题目内容
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF.

(1)求证:△FAD≌△DBC;
(2)判断△CDF的形状并证明.
【答案】(1)见解析;(2)△CDF是等腰直角三角形
【解析】
试题分析:(1)利用SAS证明△AFD和△BDC全等即可;
(2)利用全等三角形的性质得出FD=DC,即可判断三角形的形状;
解:(1)∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
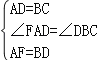 ,
,
∴△FAD≌△DBC(SAS);
(2)∵△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;

练习册系列答案
相关题目
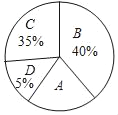
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.