ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌRtЁїABOЕФСНжБНЧБпOAЁЂOBЗжБ№дкxжсЕФИКАыжсКЭyжсЕФе§АыжсЩЯЃЌOЮЊзјБъдЕуЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈЉ3ЃЌ0ЃЉЁЂЃЈ0ЃЌ4ЃЉЃЌХзЮяЯп![]() ОЙ§ЕуBЃЌЧвЖЅЕудкжБЯпx=
ОЙ§ЕуBЃЌЧвЖЅЕудкжБЯпx=![]() ЩЯЃЎ
ЩЯЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєАбЁїABOбиxжсЯђгвЦНвЦЕУЕНЁїDCEЃЌЕуAЁЂBЁЂOЕФЖдгІЕуЗжБ№ЪЧDЁЂCЁЂEЃЌЕБЫФБпаЮABCDЪЧСтаЮЪБЃЌЪдХаЖЯЕуCКЭЕуDЪЧЗёдкИУХзЮяЯпЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгCDЃЌгыХзЮяЯпЕФЖдГЦжсНЛгкЕуPЃЌШєЕуMЪЧЯпЖЮOBЩЯЕФвЛИіЖЏЕуЃЈЕуMгыЕуOЁЂBВЛжиКЯЃЉЃЌЙ§ЕуMзїMNЁЮBDНЛxжсгкЕуNЃЌСЌНгPMЁЂPNЃЌЩшOMЕФГЄЮЊtЃЌЁїPMNЕФУцЛ§ЮЊSЃЌЧѓГіSКЭtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЌSЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГізюДѓжЕКЭДЫЪБMЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЕуCКЭЕуDЖМдкЫљЧѓХзЮяЯпЩЯЃЈ3ЃЉЕБt=
ЃЈ2ЃЉЕуCКЭЕуDЖМдкЫљЧѓХзЮяЯпЩЯЃЈ3ЃЉЕБt=![]() ЪБЃЌSШЁзюДѓжЕЪЧ
ЪБЃЌSШЁзюДѓжЕЪЧ![]() ЃЌДЫЪБЃЌЕуMЕФзјБъЮЊЃЈ0ЃЌ
ЃЌДЫЪБЃЌЕуMЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁПЗжЮіЃК(1)ЁЂЭЈЙ§ЕуBЃЈ0ЃЌ4ЃЉвдМАХзЮяЯпЕФЖдГЦжсЃЌЧѓГіКЏЪ§ЙиЯЕЪНЃЛ(2)ЁЂЭЈЙ§ЙДЙЩЖЈРэКЭСтаЮаджЪЧѓГіCЁЂDСНЕуЕФзјБъЃЌДњШыКЏЪ§ЙиЯЕЪНЧѓжЄЃЛ(3)ЁЂЭЈЙ§CЁЂDСНЕуЕФзјБъЃЌЧѓГіжБЯпCDЖдгІЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјЧѓГіЕуPЕФзјБъЃЌЭЈЙ§ЁїOMNЁзЁїOBDЧѓЕУON=![]() ЃЌдйЭЈЙ§УцЛ§ЧѓЕУSгыtЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјЧѓЕУзюДѓжЕКЭMЕуЕФзјБъЃЎ
ЃЌдйЭЈЙ§УцЛ§ЧѓЕУSгыtЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјЧѓЕУзюДѓжЕКЭMЕуЕФзјБъЃЎ
ЯъНтЃКЃЈ1ЃЉЁпХзЮяЯпy=![]() ОЙ§ЕуBЃЈ0ЃЌ4ЃЉЁрc=4ЃЌ
ОЙ§ЕуBЃЈ0ЃЌ4ЃЉЁрc=4ЃЌ
ЁпХзЮяЯпЕФЖдГЦжсЮЊ![]() ЃЌЁрЉ
ЃЌЁрЉ![]() =Љ
=Љ![]() ЃЌЁрb=Љ
ЃЌЁрb=Љ![]() ЃЛ
ЃЛ
ЁрЫљЧѓКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкRtЁїABOжаЃЌOA=3ЃЌOB=4ЃЌЁрAB=5ЃЌЁпЫФБпаЮABCDЪЧСтаЮЃЌЁрBC=CD=DA=AB=5ЃЌ
ЁрCЁЂDСНЕуЕФзјБъЗжБ№ЪЧЃЈ5ЃЌ4ЃЉЁЂЃЈ2ЃЌ0ЃЉЃЌ ЕБx=5ЪБЃЌy=![]() ЃЌ
ЃЌ
ЕБx=2ЪБЃЌy=![]() ЃЌ ЁрЕуCКЭЕуDЖМдкЫљЧѓХзЮяЯпЩЯЃЛ
ЃЌ ЁрЕуCКЭЕуDЖМдкЫљЧѓХзЮяЯпЩЯЃЛ
ЃЈ3ЃЉЩшжБЯпCDЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊy=kx+bЃЌ дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК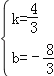 ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌy
ЪБЃЌy![]() ЃЌЁрPЃЈ
ЃЌЁрPЃЈ![]() ЃЉЃЌ ЁпMNЁЮBDЃЌ ЁрЁїOMNЁзЁїOBDЃЌ
ЃЉЃЌ ЁпMNЁЮBDЃЌ ЁрЁїOMNЁзЁїOBDЃЌ
Ёр![]() МД
МД ![]() ЕУON=
ЕУON=![]() ЃЌ ЩшЖдГЦжсНЛxгкЕуFЃЌ
ЃЌ ЩшЖдГЦжсНЛxгкЕуFЃЌ
дђ![]() =
=![]() ЃЈPF+OMЃЉOF=
ЃЈPF+OMЃЉOF=![]() ЁСЃЈ
ЁСЃЈ![]() +tЃЉЁС
+tЃЉЁС![]() ЃЌ Ёп
ЃЌ Ёп![]() ЃЌ
ЃЌ
![]() ЃЌ SЁїPMN=
ЃЌ SЁїPMN=![]() (0ЃМtЃМ4)ЃЌ
(0ЃМtЃМ4)ЃЌ
a=![]() ЃМ0ЁрХзЮяЯпПЊПкЯђЯТЃЌSДцдкзюДѓжЕЃЎ гЩSЁїPMN=
ЃМ0ЁрХзЮяЯпПЊПкЯђЯТЃЌSДцдкзюДѓжЕЃЎ гЩSЁїPMN=![]() ЃЌ
ЃЌ
ЁрЕБt=![]() ЪБЃЌSШЁзюДѓжЕЪЧ
ЪБЃЌSШЁзюДѓжЕЪЧ![]() ЃЌДЫЪБЃЌЕуMЕФзјБъЮЊЃЈ0ЃЌ
ЃЌДЫЪБЃЌЕуMЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ




