��Ŀ����
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ�������Σ�
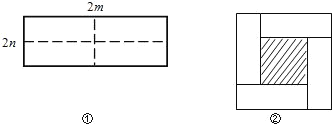
��1������Ϊͼ���е���Ӱ���ֵ������εı߳�����_________________��
��2���������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ������
������ __________________�������� _____________________��
��3���۲�ͼ�ڣ�����д��(m+n)2��(m-n)2��mn����������ʽ֮��ĵ�����ϵ��
��________________________ .
��4�����ݣ�3�����еĵ�����ϵ������������⣺��a+b=6��ab=4������(a-b)2��ֵ��
���𰸡���1��m-n����2����m+n��2-4mn��m-n��2����3����m+n��2-4mn=��m-n��2����4��20��
��������
ƽ���ֳɺ�ÿ��С�����εij�Ϊm����Ϊn��
��1�������εı߳�=С�����εij�-����
��2����һ�ַ���Ϊ�������������-4��С������������ڶ��ֱ�ʾ����Ϊ����Ӱ����ΪС�����ε������
��3�����ã�m+n��2-4mn=��m-n��2����⣻
��4�����ã�a-b��2=��a+b��2-4ab����⣮
��1��m-n��
��2����m+n��2-4mn��m-n��2��
��3����m+n��2-4mn=��m-n��2��
��4����a-b��2=��a+b��2-4ab��
��a+b=6��ab=4��
�ࣨa-b��2=36-16=20��