题目内容
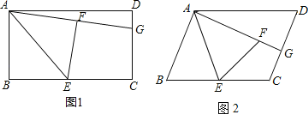
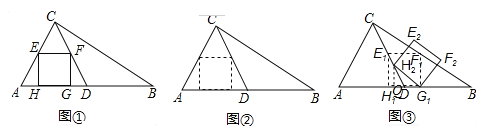
【题目】(2016湖南省益阳市)如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为![]() 时,求矩形平移的距离;
时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.

【答案】答案见解析.
【解析】试题分析:(1)根据已知,由直角三角形的性质可知AB=2,从而求得AD,CD,利用中位线的性质可得EF,DF,利用三角函数可得GF,由矩形的面积公式可得结果;
(2)首先利用分类讨论的思想,分析当矩形与△CBD重叠部分为三角形时(0<x≤![]() ),利用三角函数和三角形的面积公式可得结果;当矩形与△CBD重叠部分为直角梯形时(
),利用三角函数和三角形的面积公式可得结果;当矩形与△CBD重叠部分为直角梯形时(![]() <x≤
<x≤![]() ),列出方程解得x;
),列出方程解得x;
(3)作H2Q⊥AB于Q,设DQ=m,则H2Q=![]() ,又
,又![]() ,
,![]() ,利用勾股定理可得m,在Rt△QH2G1中,利用三角函数解得cosα.
,利用勾股定理可得m,在Rt△QH2G1中,利用三角函数解得cosα.
试题解析:(1)如图①,在△ABC中,∵∠ACB=90°,∠B=30°,AC=1,∴AB=2,
又∵D是AB的中点,∴AD=1,CD=![]() AB=1,
AB=1,
又∵EF是△ACD的中位线,∴EF=DF=![]() ,
,
在△ACD中,AD=CD,∠A=60°,∴∠ADC=60°,
在△FGD中,GF=DFsin60°=![]() ,∴矩形EFGH的面积S=EFGF=
,∴矩形EFGH的面积S=EFGF=![]() =
=![]() ;
;
(2)如图②,设矩形移动的距离为x,则0<x≤![]() ;
;
当矩形与△CBD重叠部分为三角形时,则0<x≤![]() ,S=
,S=![]() ,∴x=
,∴x=![]() .(舍去);
.(舍去);
当矩形与△CBD重叠部分为直角梯形时,则![]() <x≤
<x≤![]() ,重叠部分的面积S=
,重叠部分的面积S=![]() ,∴x=
,∴x=![]() ,即矩形移动的距离为
,即矩形移动的距离为![]() 时,矩形与△CBD重叠部分的面积是
时,矩形与△CBD重叠部分的面积是![]() ;
;
(3)如图③,作H2Q⊥AB于Q,设DQ=m,则H2Q=![]() ,又
,又![]() ,
,![]() .
.
在Rt△H2QG1中,![]() ,解之得m=
,解之得m=![]() (负的舍去),
(负的舍去),
∴cosα=![]() =
=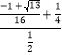 =
=![]() .
.

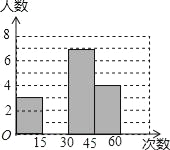
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?