Question

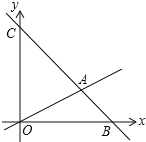
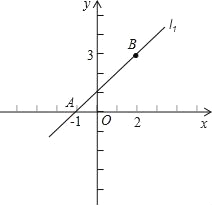
【题目】如图，已知直线l1：y=kx+1，与x轴相交于点A，同时经过点B（2，3），另一条直线l2经过点B，且与x轴相交于点P（m，0）．

（1）求l1的解析式；

（2）若S△APB=3，求P的坐标．

Answer 1

【答案】（1）直线l1对应的函数表达式y=x+1；（2）P（﹣3，0）或（1，0）．

【解析】

（1）设直线L1的解析式为y=kx+b，由题意列出方程组求解；
（2）分两种情形，即点P在A的左侧和右侧分别求出P点坐标．

（1）∵y=kx+1，经过点B（2，3），

∴3=2k+1，

∴k=1，

∴直线l1对应的函数表达式y=x+1，

（2）∵A（﹣1，0），

△APB的面积= PA3=3，

解得PA=2，

当点P在点A的左边时，OP=OA+PA=1+2=3，

此时m=﹣3，

当点P在点A的右边时，OP=PA﹣OA=2﹣1=1，

此时m=1，

综上所述，P（﹣3，0）或（1，0）．