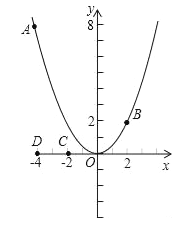
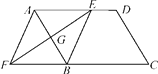
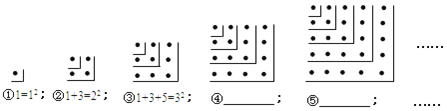
题目内容
【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系
小颖同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
请你参考小颖同学的思路,探究并解决下列问题:
(1)请你写出上面问题中线段PG与PC的位置关系;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题申的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
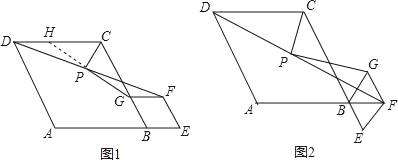
【答案】(1)线段PG与PC的位置关系是PG⊥PC,理由见解析;(2)猜想:(1)中的结论没有发生变化,证明见解析.
【解析】试题分析:(1)根据题意可知小颖的思路为,通过判定三角形DHP和PGF为全等三角形来得出证明三角形HCG为等腰三角形且P为底边中点的条件;
(2)思路同上,延长GP交AD于点H,连接CH,CG,本题中除了如(1)中证明△GFP≌△HDP(得到P是HG中点)外还需证明△HDC≌△GBC(得出三角形CHG是等腰三角形).
试题解析:(1)线段PG与PC的位置关系是PG⊥PC.
理由:延长GP,交CD于点H,
∵四边形ABCD与四边形BEFG是菱形,
∴CD∥AB∥GF,
∴∠PDH=∠PFG,∠DHP=∠PGF,
∵P是线段DF的中点,
∴DP=PF,
在△DPH和△FGP中,
 ,
,
∴△DPH≌△FGP(AAS),
∴PH=PG,DH=GF,
∵CD=BC,GF=GB=DH,
∴CH=CG,
∴CP⊥HG,
即PG⊥PC;
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP交AD于点H,连接CH,CG,
∵P是线段DF的中点,
∴FP=DP,
∵AD∥FG,
∴∠GFP=∠HDP.
又∠GPF=∠HPD,
∴△GFP≌△HDP
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,∠HDC=∠ABC=60°.
由∠ABC=∠BEF=60°,且菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,
∴∠GBC=60°.
∴∠HDC=∠GBC.
∵四边形BEFG是菱形,
∴GF=GB.
∵△HDC≌△GBC.
∴CH=CG.
∴PH=PG,PG⊥PC.


【题目】①若![]() ,则
,则![]() ;②整数和分数统称为有理数;③绝对值等于它本身的整数是0;④
;②整数和分数统称为有理数;③绝对值等于它本身的整数是0;④![]() 是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数,其中判断正确的有( )
是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数,其中判断正确的有( )
A.1个B.2个C.3个D.4个
【题目】我国是水资源比较贫乏的国家之一,为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段来达到节约用水的目的,规定如下用水收费标准:每户每月的用水不超过20立方米(含20立方米)时,水费按“基本价”收费:超过20立方米时,不超过的部分仍按“基本价”收费,超过部分按“调节价”收费.某户居民今年4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
4 | 20 | 42 |
5 | 24 | 56.40 |
(1)请你算一算该市水费的“调节价”每立方米多少元?
(2)若该户居民6月份用水量为30立方米,请算一算,6月份水费是多少元?