Question

【题目】如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．

（1）求证：BG∥CD；

（2）设△ABC外接圆的圆心为O，若AB=DH，∠OHD=80°，求∠BDE的大小．

Answer 1

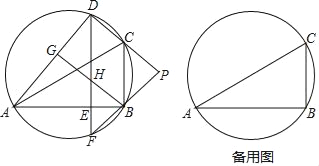
【答案】（1）证明见解析；（2）∠BDE的度数为20°或40°．

【解析】

（1）PC=PB，得到∠PCB=∠PBC，根据圆内接四边形的性质，得到∠BAD+∠BCD=180°，根据同角的补角相等得到∠BAD=∠PCB，根据圆周角定理得到∠BAD=∠BFD，等量代换得到∠BFD=∠PCB=∠PBC，即可证明BC∥DF，根据AC是⊙O的直径，得到

∠ADC=90°，根据BG⊥AD，得到∠ADC=∠AGB，即可证明BG∥CD；

（2）分①当点O在DE的左侧和②当点O在DE的右侧两种情况进行讨论.

（1）证明：如图1，

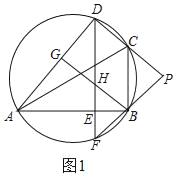
∵PC=PB，

∴∠PCB=∠PBC，

∵四边形ABCD内接于圆，

∴∠BAD+∠BCD=180°，

∵∠BCD+∠PCB=180°，

∴∠BAD=∠PCB，

∵∠BAD=∠BFD，

∴∠BFD=∠PCB=∠PBC，

∴BC∥DF，

∵DE⊥AB，

∴∠DEB=90°，

∴∠ABC=90°，

∴AC是⊙O的直径，

∴∠ADC=90°，

∵BG⊥AD，

∴∠AGB=90°，

∴∠ADC=∠AGB，

∴BG∥CD；

（2）由（1）得：BC∥DF，BG∥CD，

∴四边形BCDH是平行四边形，

∴BC=DH，

在Rt△ABC中，∵

∴tan∠ACB=

∴∠ACB=60°，∠BAC=30°，

∴∠ADB=60°，

∴

①当点O在DE的左侧时，如图2，作直径DM，连接AM、OH，则∠DAM=90°，

∴∠AMD+∠ADM=90°

∵DE⊥AB，

∴∠BED=90°，

∴∠BDE+∠ABD=90°，

∵∠AMD=∠ABD，

∴∠ADM=∠BDE，

∵

∴DH=OD，

∴∠DOH=∠OHD=80°，

∴∠ODH=20°

∵∠ADB=60°，

∴∠ADM+∠BDE=40°，

∴∠BDE=∠ADM=20°，

②当点O在DE的右侧时，如图3，作直径DN，连接BN，

由①得：∠ADE=∠BDN=20°，∠ODH=20°，

∴∠BDE=∠BDN+∠ODH=40°，

综上所述，∠BDE的度数为20°或40°．