题目内容
【题目】已知抛物线![]() 与 y 轴交于点 C(0,4),与 x 轴交于点 A、B,点 A 的坐标为(4,0).
与 y 轴交于点 C(0,4),与 x 轴交于点 A、B,点 A 的坐标为(4,0).
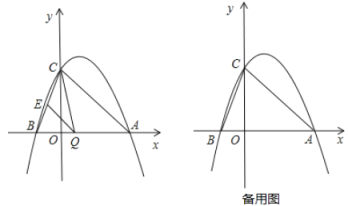
(1)求此抛物线的解析式;
(2)点 Q 是线段 AB 上的动点,过点 Q 作 QE∥AC,交 BC 于点 E,连接 CQ,当△CQE 的面积最大时,求点 Q的坐标;
(3)当点 Q 从点 B 出发沿着 BA 方向以每秒 2 个单位长向点 A 运动,同时点 P 从点 A 出发沿着 AC 方向以每秒 ![]() 个单位长度向点 C 运动,其中一个点到达终点,另一个点也停止运动,设 P、Q 运动时间为 t 秒,当 t 为何值?△APQ为等腰三角形?
个单位长度向点 C 运动,其中一个点到达终点,另一个点也停止运动,设 P、Q 运动时间为 t 秒,当 t 为何值?△APQ为等腰三角形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 秒或
秒或![]() 秒或2秒.
秒或2秒.
【解析】
(1)根据抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,用待定系数法求出
,用待定系数法求出![]() ,
,![]() 的值,即可求出该抛物线的解析式;
的值,即可求出该抛物线的解析式;
(2)设![]() ,因为
,因为![]() ,所以
,所以![]() ,再利用相似三角形的性质得出
,再利用相似三角形的性质得出![]() ,进而可得
,进而可得![]() ,然后利用二次函数的性质求出点
,然后利用二次函数的性质求出点![]() 的坐标;
的坐标;
(3)分别用t的式子表示出![]() 的边长,再在
的边长,再在![]() 中分三种情况①
中分三种情况①![]() ,②
,②![]() ,③
,③![]() 构建方程求出t值即可.
构建方程求出t值即可.
解:(1)![]() 抛物线
抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
![]()
![]() ,
,
解得: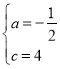 ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ;
;
(2)![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
解得![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,0,
,0,![]() ,
,![]() ,
,
![]() .
.
设![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
当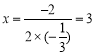 时,
时,![]() 面积最大,
面积最大,
![]()
![]() 点坐标为
点坐标为![]() .
.
(3)依题意得:BQ=2t,AP=![]() ,
,
∴AQ=6-2t,
∵OC=OA=4,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴∠CAO=45°,
在![]() 中分三种情况;
中分三种情况;
①当![]() 时,如图1,
时,如图1,
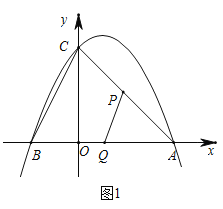
则![]() ,解得:
,解得:![]() ,
,
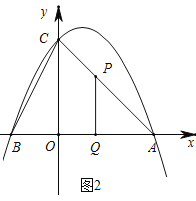
②当AP=PQ时,如图2,
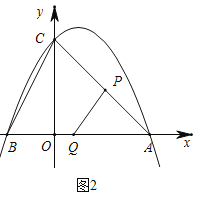
∵∠CAO=45°,∴∠APQ=90°,
∴![]() ,即
,即![]() ,解得
,解得![]()
③当AQ=PQ时,如图3,
∵∠CAO=45°,
∴∠AQP=90°,
∴![]() ,即
,即![]() ,解得
,解得![]()
综上所述:使得![]() 是等腰三角形,则t的值为:
是等腰三角形,则t的值为:![]() 秒或
秒或![]() 秒或2秒.
秒或2秒.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天.两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.两个厂家销售情况如下表:
甲厂家销量(件) | 38 | 39 | 40 | 41 | 42 |
天数 | 2 | 4 | 2 | 1 | 1 |
乙厂家销量(件) | 38 | 39 | 40 | 41 | 42 |
天数 | 1 | 2 | 2 | 4 | 1 |
(1)现从乙厂家试销的10天中随机抽取1天,求这1天的返利不超过160元的概率;
(2)商场拟甲、乙两个厂家中选择一个长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.