题目内容
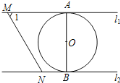
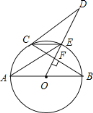
【题目】已知,如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 点的切线交
点的切线交![]() 的延长线于点
的延长线于点![]() .下列结论:
.下列结论:
①![]() ;②两段劣弧
;②两段劣弧![]() =
=![]() ;③
;③![]() 与
与![]() 相切;④
相切;④![]() .
.
其中一定正确的有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
①由等腰三角形性质得到∠OEB=∠ABC=∠ACB,从而可得OE∥AC;
②连接OD,由平行线的性质和等腰三角形的性质证得∠BOE=∠EOD,从而得到![]() =
=![]() ;
;
③由SAS证得△OBF≌△ODF,即可得到∠OBF=∠ODF.根据切线的性质可得∠OBF=90°,则有∠ODF=90°,即可得到DF与⊙O相切;
④由OE∥AC,得出△BOE∽△BAC,根据相似三角形的性质即可得到![]() =(
=(![]() )2=
)2=![]() ,△BDE的面积≠△BOE的面积,得出④不一定正确,即可得出结论.
,△BDE的面积≠△BOE的面积,得出④不一定正确,即可得出结论.
①∵AB=AC,OB=OE,∴∠ABC=∠ACB,∠OBE=∠OEB,∴∠OEB=∠ACB,∴OE∥AC,故①正确;
②连接OD,如图所示:
∵OE∥AC,∴∠BOE=∠OAD,∠EOD=∠ADO.
∵OA=OD,∴∠OAD=∠ODA,∴∠BOE=∠EOD,∴![]() =
=![]() ,故②正确;
,故②正确;
③在△OBF和△ODF中,∵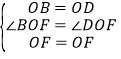 ,∴△OBF≌△ODF(SAS),∴∠OBF=∠ODF.
,∴△OBF≌△ODF(SAS),∴∠OBF=∠ODF.
∵BF与⊙O相切于点B,∴∠OBF=90°,∴∠ODF=90°,∴DF与⊙O相切,故③正确;
④∵OE∥AC,∴△BOE∽△BAC,∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,而△BDE的面积≠△BOE的面积,故④不正确;正确的有3个.
,而△BDE的面积≠△BOE的面积,故④不正确;正确的有3个.
故选C.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目