题目内容
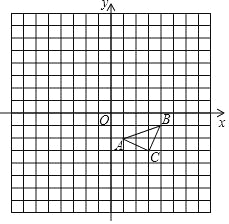
【题目】如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,﹣2),B(4,﹣1),C(3,﹣3)(正方形网格中,每个小正方形的边长都是1个单位长度).
(1)作出△ABC向左平移5个单位长度,再向下平移3个单位长度得到的△A1B1C1;
(2)以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A2B2C2作出△A2B2C2;
(3)以坐标原点O为旋转中心,将△ABC逆时针旋转90°,得到△A3B3C3,作出△A3B3C3,并求线段AC扫过的面积.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)将三顶点分别向左平移5个单位长度,再向下平移3个单位长度得到的对应点,顺次连接可得;
(2)根据位似图形的定义作出对应点,顺次连接可得;
(3)将三顶点分别绕点O逆时针旋转90°得到对应点,顺次连接可得:再根据扇形面积公式计算可得.
(1)如图,△A1B1C1即为所求;
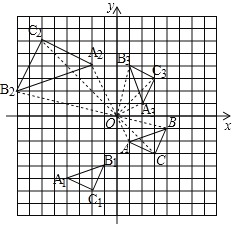
(2)如图,△A2B2C2即为所求;
(3)如图,△A3B3C3即为所求.
∵OA=![]() =
=![]() ,OC=
,OC=![]() =3
=3![]() ,∴线段AC扫过的面积为
,∴线段AC扫过的面积为![]() ﹣
﹣![]() =
=![]() π.
π.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目