��Ŀ����
����Ŀ����1�����ⱳ��
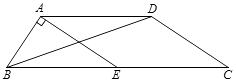
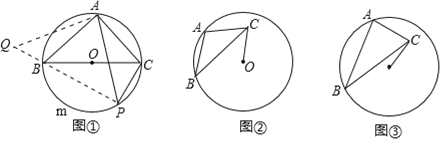
��ͼ�٣�BC�ǡ�O��ֱ������A�ڡ�O�ϣ�AB=AC��PΪBmC��һ���㣨����B��C�غϣ�����֤�� ![]() PA=PB+PC��
PA=PB+PC��
С��ͬѧ�۲쵽ͼ���Ե�A�����������߶�AB��AP��AC����AB=AC�����Ϊ��ת�����̵森���ǣ�С��ͬѧ������˼�����̣�
��һ��������PAC���ŵ�A˳ʱ����ת90������QAB����ͼ�٣���
�ڶ�����֤��Q��B��P���㹲�ߣ�����ԭ���֤��
�������С��ͬѧ��˼���������֤�����̣�
��2�����Ǩ��
��ͼ�ڣ���O�İ뾶Ϊ3����A��B�ڡ�O�ϣ�CΪ��O��һ�㣬AB=AC��AB��AC������ΪA����OC����Сֵ��
��3����չ����
��ͼ�ۣ���O�İ뾶Ϊ3����A��B�ڡ�O�ϣ�CΪ��O��һ�㣬AB=![]() AC��AB��AC������ΪA����OC����СֵΪ�� ����
AC��AB��AC������ΪA����OC����СֵΪ�� ����
���𰸡���1��֤������������2��OC��Сֵ��3![]() ��3����3��
��3����3��![]() ��
��
�������������������1������PAC���ŵ�A˳ʱ����ת90������QAB����ͼ�٣���ֻҪ֤����APQ�ǵ���ֱ�������μ��ɽ�����⣻
��2����ͼ���У�����OA������OAC�Ƶ�O˳ʱ����ת90������QAB������OB��OQ���ڡ�BOQ�У��������߹�ϵ�������ɽ�����⣻
��3����ͼ�۹������������μ��ɽ�����⣮��AQ��OA��ʹ��AQ=![]() OA������OQ��BQ��OB���ɡ�QAB��OAC���Ƴ�BQ=
OA������OQ��BQ��OB���ɡ�QAB��OAC���Ƴ�BQ=![]() OC����BQ��Сʱ��OC��С��
OC����BQ��Сʱ��OC��С��
�����������1������PAC���ŵ�A˳ʱ����ת90������QAB����ͼ�٣���
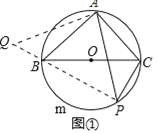
��BC��ֱ�������BAC=90�㣬
��AB=AC�����ACB=��ABC=45�㣬
����ת�ɵá�QBA=��PCA����ACB=��APB=45�㣬PC=QB��
�ߡ�PCA+��PBA=180�㣬���QBA+��PBA=180�㣬��Q��B��P���㹲�ߣ�
���QAB+��BAP=��BAP+��PAC=90�㣬��QP2=AP2+AQ2=2AP2��
��QP=![]() AP=QB+BP=PC+PB����
AP=QB+BP=PC+PB����![]() AP=PC+PB��
AP=PC+PB��
��2����ͼ���У�����OA������OAC�Ƶ�A˳ʱ����ת90������QAB������OB��OQ��

��AB��AC,���BAC=90��,
����ת�ɵá�QB=OC��AQ=OA����QAB=��OAC�����QAB+��BAO=��BAO+��OAC=90�㣬
����Rt��OAQ�У�OQ=3![]() ��AO=3 �����ڡ�OQB�У�BQ��OQ��OB=3
��AO=3 �����ڡ�OQB�У�BQ��OQ��OB=3![]() ��3 ��
��3 ��
��OC��Сֵ��3![]() ��3��
��3��
��3����ͼ���У���AQ��OA��ʹ��AQ=![]() OA������OQ��BQ��OB��
OA������OQ��BQ��OB��
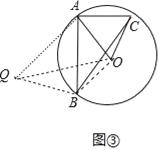
�ߡ�QAO=��BAC=90�㣬��QAB=��OAC����![]() =
=![]() ��
��
���QAB��OAC����BQ=![]() OC��
OC��
��BQ��Сʱ��OC��С����֪OA=3��AQ=4��OQ=5��BQ��OQ��OB����OQ��2��]
��BQ����СֵΪ2��
��OC����СֵΪ![]() ��2=
��2=![]() ��
��
�ʴ�Ϊ![]() ��
��