题目内容
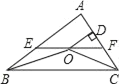
【题目】已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为![]() 的中点.
的中点.
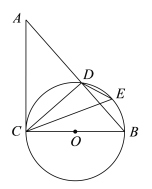
(1)求证:∠ACD=∠DEC;(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长
【答案】(1)见解析;(2)PE=4.
【解析】
(1)根据同角的余角相等得到∠ACD=∠B,然后由圆周角定理可得结论;
(2)连结OE,根据圆周角定理和等腰三角形的性质证明OE∥CD,然后由△POE∽△PCD列出比例式,求解即可.
解:(1)证明:∵BC是⊙O的直径,
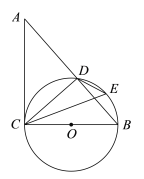
∴∠BDC=90°,∴∠BCD+∠B=90°,
∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∴∠ACD=∠B,
∵∠DEC=∠B,
∴∠ACD=∠DEC
(2)证明:连结OE
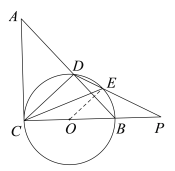
∵E为BD弧的中点.
∴∠DCE=∠BCE
∵OC=OE
∴∠BCE=∠OEC
∴∠DCE=∠OEC
∴OE∥CD
∴△POE∽△PCD,
∴![]()
∵PB=BO,DE=2
∴PB=BO=OC
∴![]()
∴![]()
∴PE=4

练习册系列答案
相关题目
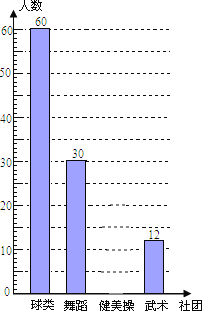
【题目】为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
社团类别 | 人数 | 占总人数比例 |
球类 | 60 | m |
舞蹈 | 30 | 0.25 |
健美操 | n | 0.15 |
武术 | 12 | 0.1 |
(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.