题目内容
【题目】（题文）如图，AB是
的直径，且
，点M为外一点，且MA，MC分别切于点A、C两点
与AM的延长线交于点D．
求证：
；
填空
当
______时，四边形AOCM是正方形．
当______时，
为等边三角形．
【答案】（1）证明见解析；（2）
3；
【解析】
根据切线的性质得：
，
，证明
≌
，得
，根据等边对等角得：
，由等角的余角相等可得结论；
①直接可得
；
②先根据等边三角形定义可得：
，
，证明
≌
，得
，可得结论．
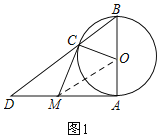
解：如图1，连接OM，
，MC分别切
于点A、C，
，，
在
和
中，
∵
，
，
≌，
，
，
，
又
，
，
，
，
；
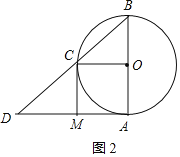
①如图2，当时，四边形AOCM是正方形；
，
四边形AOCM是菱形，
又
，
四边想AOCM是正方形；
②连接OM，如图3，
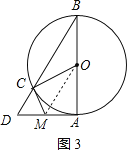
是等边三角形，
，，
，
，
，
，
，
，
设
，
，
，
≌，
，
；
故答案为：①
；②
．
练习册系列答案
相关题目
