题目内容
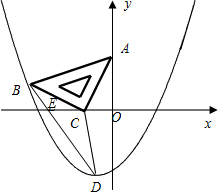
如图,平面直角坐标系中,Rt△OAB的OA边在x轴上,OB边在y轴上,且OA=2,A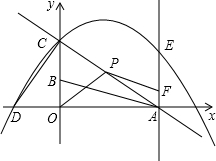 B=
B=
,将△OAB绕点O逆时针方向旋转90°后得△OCD,已知点E的坐标是(2、2)
(1)求经过D、C、E点的抛物线的解析式;
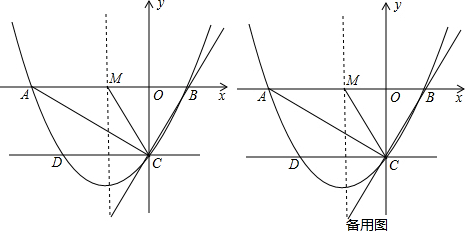
(2)点M(x、y)是抛物线上任意点,当0<x<2时,过M作x轴的垂线交直线AC于N,试探究线段MN是否存在最大值,若存在,求出最大值是多少?并求出此时M点的坐标;
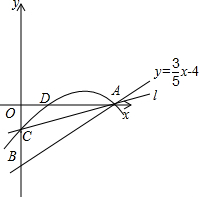
(3)P为直线AC上一动点,连接OP,作PF⊥OP交直线AE于F点,是否存在点P,使△PAF是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
 B=
B=| 5 |
(1)求经过D、C、E点的抛物线的解析式;
(2)点M(x、y)是抛物线上任意点,当0<x<2时,过M作x轴的垂线交直线AC于N,试探究线段MN是否存在最大值,若存在,求出最大值是多少?并求出此时M点的坐标;
(3)P为直线AC上一动点,连接OP,作PF⊥OP交直线AE于F点,是否存在点P,使△PAF是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)在Rt△AOB中,AB=
,OA=2,由勾股定理得:OB=1;
由于△ODC是由△OBA旋转90°所得,
所以OB=OD=1,OA=OC=2,
因此D(-1,0),C(0,2),A(2,0),
∵E(2,2),
设抛物线的解析式为:y=ax2+bx+c,则有:
,
解得
;
∴抛物线的解析式为:y=-
x2+
x+2.
(2)∵A(2,0),C(0,2),
∴直线AC:y=-x+2;
∴M(x,-
x2+
x+2),N(x,-x+2);
故MN=-
x2+
x+2-(-x+2)=-
x2+
x=-
(x-
)2+
,
因此当x=1,即M(
,
)时,MN取最大值,且最大值为
.
(3)由于P在直线AC上,
所以设P(a,-a+2)(a≠1且a≠2),
则直线OP:y=
x;
由于PF⊥OP,可设直线PF:y=
x+h,则有:
×a+h=-a+2,h=-a+2-
=
,
即直线PF:y=
x+
;
当x=2时,y=
=-2a+2;
∴P(a,-a+2),F(2,-2a+2),A(2,0),
∴PF2=(a-2)2+a2,PA2=(2-a)2+(a-2)2=2(a-2)2,AF2=(-2a+2)2,
①当PF=PA时,PF2=PA2,则有:
(a-2)2+a2=2(a-2)2,
解得a=1(不合题意,舍去);
故此种情况不成立;
②当PF=AF时,PF2=AF2,则有:
(a-2)2+a2=(-2a+2)2,
解得a=0,a=2(舍去),
∴P(0,2);
③当PA=AF时,PA2=AF2,则有:
2(a-2)2=(-2a+2)2,
解得a=±
,
∴P(
,2-
)或P(-
,2+
);
综上所述,存在符合条件的P点,且坐标为:P1(0,2),P2(
,2-
),P3(-
,2+
).
| 5 |
由于△ODC是由△OBA旋转90°所得,
所以OB=OD=1,OA=OC=2,
因此D(-1,0),C(0,2),A(2,0),
∵E(2,2),
设抛物线的解析式为:y=ax2+bx+c,则有:
|
解得
|
∴抛物线的解析式为:y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)∵A(2,0),C(0,2),
∴直线AC:y=-x+2;
∴M(x,-
| 2 |
| 3 |
| 4 |
| 3 |
故MN=-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 2 |
| 3 |
| 7 |
| 4 |
| 49 |
| 24 |
因此当x=1,即M(
| 7 |
| 4 |
| 55 |
| 24 |
| 49 |
| 24 |
(3)由于P在直线AC上,
所以设P(a,-a+2)(a≠1且a≠2),
则直线OP:y=
| 2-a |
| a |
由于PF⊥OP,可设直线PF:y=
| a |
| a-2 |
| a |
| a-2 |
| a2 |
| a-2 |
| -2a2+4a-4 |
| a-2 |
即直线PF:y=
| a |
| a-2 |
| -2a2+4a-4 |
| a-2 |
当x=2时,y=
| 2a-a2+4a-4 |
| a-2 |
∴P(a,-a+2),F(2,-2a+2),A(2,0),
∴PF2=(a-2)2+a2,PA2=(2-a)2+(a-2)2=2(a-2)2,AF2=(-2a+2)2,
①当PF=PA时,PF2=PA2,则有:
(a-2)2+a2=2(a-2)2,
解得a=1(不合题意,舍去);
故此种情况不成立;
②当PF=AF时,PF2=AF2,则有:
(a-2)2+a2=(-2a+2)2,
解得a=0,a=2(舍去),
∴P(0,2);
③当PA=AF时,PA2=AF2,则有:
2(a-2)2=(-2a+2)2,
解得a=±
| 2 |
∴P(
| 2 |
| 2 |
| 2 |
| 2 |
综上所述,存在符合条件的P点,且坐标为:P1(0,2),P2(
| 2 |
| 2 |
| 2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目