题目内容
某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R、P与x的关系式分别为R=500+30x,P=170-2x.
(1)当日产量为多少时,每日获得的利润为1750元?
(2)当日产量为多少时,可获得最大利润?最大利润是多少?
(1)当日产量为多少时,每日获得的利润为1750元?
(2)当日产量为多少时,可获得最大利润?最大利润是多少?
(1)∵生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R,P与x的关系式分别为R=500+30x,P=170-2x,
∴(170-2x)x-(500+30x)=1750,
解得 x1=25,x2=45(大于每日最高产量为40只,舍去).
(2)设每天所获利润为W,
由题意得,W=(170-2x)x-(500+30x)
=-2x2+140x-500
=-2(x2-70x)-500
=-2(x2-70x+352-352)-500
=-2(x2-70x+352)+2×352-500
=-2(x-35)2+1950.
当x=35时,W有最大值1950元.
答:当日产量为25只时,每日获得利润为1750元;要想获得最大利润,每天必须生产35个工艺品,最大利润为1950.
∴(170-2x)x-(500+30x)=1750,
解得 x1=25,x2=45(大于每日最高产量为40只,舍去).
(2)设每天所获利润为W,
由题意得,W=(170-2x)x-(500+30x)
=-2x2+140x-500
=-2(x2-70x)-500
=-2(x2-70x+352-352)-500
=-2(x2-70x+352)+2×352-500
=-2(x-35)2+1950.
当x=35时,W有最大值1950元.
答:当日产量为25只时,每日获得利润为1750元;要想获得最大利润,每天必须生产35个工艺品,最大利润为1950.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
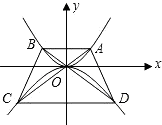 抛物线y=-
抛物线y=-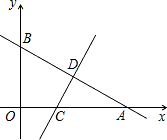 的垂直平分线交x轴于点C,交AB于点D.
的垂直平分线交x轴于点C,交AB于点D.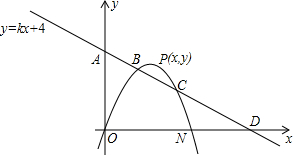 A的面积等于△PON面积的
A的面积等于△PON面积的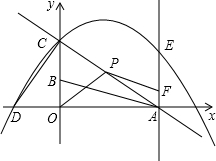 B=
B=
 金150万元,请问能否将这30户移民农户全部安置?并说明理由.
金150万元,请问能否将这30户移民农户全部安置?并说明理由.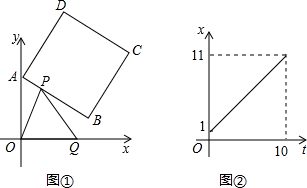 能,写出所有符合条件的t的值;若不能,请说明理由.
能,写出所有符合条件的t的值;若不能,请说明理由.