题目内容
将二次函数y=2x2-8x-5的图象沿它的对称轴所在直线向上平移，得到一条新的抛物线，这条新的抛物线与直线y=kx+1有一个交点为（3，4）．
求：（1）新抛物线的解析式及后的值；
（2）新抛物线与y=kx+1的另一个交点的坐标．
求：（1）新抛物线的解析式及后的值；
（2）新抛物线与y=kx+1的另一个交点的坐标．
（1）y=2x2-8x-5=2（x2-4x）-5=2（x-2）2-13，
设新抛物线为：y=2（x-2）2+m，
由题意知：（3，4）为新抛物线与直线的交点，
则4=2（3-2）2+m，
∴m=2，
又4=3k+1，
∴k=1，
∴新抛物的解析式为：y=2（x-2）2+2；
（2）当直线与新抛物相交时，则2（x-2）2+2=x+1，
∴x1=3，x2=
，
∴另一个交点为：（
，
）．
设新抛物线为：y=2（x-2）2+m，
由题意知：（3，4）为新抛物线与直线的交点，
则4=2（3-2）2+m，
∴m=2，
又4=3k+1，
∴k=1，
∴新抛物的解析式为：y=2（x-2）2+2；
（2）当直线与新抛物相交时，则2（x-2）2+2=x+1，
∴x1=3，x2=
| 3 |
| 2 |
∴另一个交点为：（
| 3 |
| 2 |
| 5 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
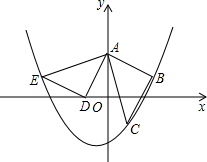B（2，1），C（1，-1），将三角板绕A点顺时针转α°后，使B点与x轴上的点D（-1，0）重合．
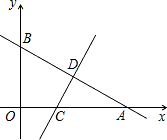的垂直平分线交x轴于点C，交AB于点D．
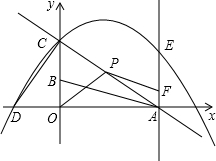B=
金150万元，请问能否将这30户移民农户全部安置？并说明理由．
能，写出所有符合条件的t的值；若不能，请说明理由．