��Ŀ����
����Ŀ�����һ����������һ�����ϵĸߵ��������ߵ�һ�룬��ô���ǰ���������ν������������������
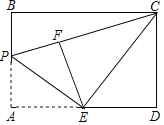
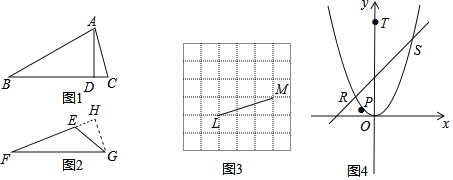
��ͼ1��������ABC��BC���ϵĸ�AD����BC��һ�룬��ABC���ǰ�������Σ���ʱ������ABC��BC���������Σ���ͼ2��������EFG��EF���ϵĸ�GH����EF��һ�룬��EFG���ǰ�������Σ���ʱ������EFG��EF���������Σ�
��1��ֱ��д������3��С��Ĵ𰸣�
����һ�������μ��ǵ������������ǰ�������Σ�����Ƕ��������п���ֵΪ�� ��
����һ�������μ���ֱ�����������ǰ�������Σ�������С�ǵ�����ֵΪ�� ��
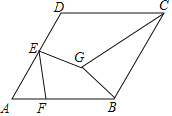
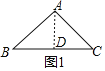
����ͼ3�������������У�L��M����֪��������㣬�����Nʹ����LMNΪ��������Σ�����LMNΪ���������λ�ֱ�������Σ��������ĸ��N������ ����
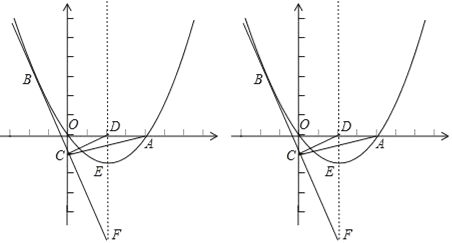
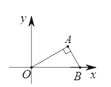
��2����ͼ��ƽ��ֱ������ϵ�ڣ�ֱ��y��x+2��������y��x2����R��S���㣬��T����Ϊ��0��5������P��������y��x2�ϵ�һ�����㣬��Q������ϵ��һ�㣬��ʹ����RSQΪRS���������Σ�
�ٵ���P���ڵ�R���S֮�䣨������R��S������PQȡ����Сֵʱ�����P�����꣮
�ڵ���P���ڵ�R���O֮�䣨������R��O��ʱ����PQ+![]() QT����Сֵ��
QT����Сֵ��
���𰸡���1����45�㡢15�㡢75�㣻��1��![]() ����7�� ��2���ٵ�P�䣨
����7�� ��2���ٵ�P�䣨![]() ��
��![]() ������ʱ��P��P�䣩Qȡ����Сֵ���ڵ���P���R�غϣ���P��Q��H��һ��ֱ������ֱ��HT��ֱʱ��PQ+
������ʱ��P��P�䣩Qȡ����Сֵ���ڵ���P���R�غϣ���P��Q��H��һ��ֱ������ֱ��HT��ֱʱ��PQ+![]() QT����Сֵ����СֵΪ4��
QT����Сֵ����СֵΪ4��
��������
��1���٢ڷֵױ��ϵĸߵ��ڵױߵ�һ�롢���ϵĸߵ���������һ����������ֱ���⼴�ɣ�����ͼ3�������ĸ��N����7����
��2������ͼ4������P���ڵ�R���S֮��ʱ����RSƽ������������ֻ��һ������P��ʱ��PQȡ����Сֵ��������⣻�ڵ���P���R�غϣ���P��Q��H��һ��ֱ������ֱ��HT��ֱʱ��PQ+![]() QT����Сֵ��������⣮
QT����Сֵ��������⣮
��1���ٵ��ױ��ϵĸߵ��ڵױߵ�һ��ʱ��
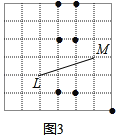
����ͼ��ABCΪ���������Σ�AB��AC��AD��![]() BC��
BC��
��AD��CD�����B����C��45����
�����ϵĸߵ���������һ��ʱ��
ͬ����Ϊ75����15����
�ʣ���Ϊ45����15����75����
�ڵ��ױ��ϵĸߵ��ڵױߵ�һ��ʱ������ͼ����ABCΪ����ֱ�������Σ�
����С��Ϊ45������С�ǵ�����ֵΪ1��
���ϵĸߵ���������һ��ʱ��ͬ���ɵã���С�ǵ�����ֵΪ![]() ��
��
�ʴ�Ϊ1��![]() ��
��
����ͼ3�������ĸ��N����7���������������ͼ��С�ڵ���ʾ��λ�ã�
��2������������ֱ�߷�����������ã�x����1��2��
������R��S������ֱ�Ϊ����1��1������2��4������RS��![]() ��
��
��RS���ϵĸ�Ϊ![]() ��
��
���Q����RSƽ�е���������ֱ���ϣ�����ͼ��
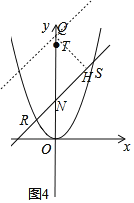
����Q��QH��NH���ڵ�H����HQ��![]() ����QN��
����QN��![]() ��3��
��3��
��N��0��2�������M��5��0������M�ڵ�T�غϣ�
���Q��ֱ�߷���Ϊ��y��x+5��
����ֱ����ֱ��RS���·�ʱ��y��x��1��
�ʵ�Q���ڵ�ֱ�߷���Ϊ��y��x+5��y��x��1��
����ͼ4������P���ڵ�R���S֮��ʱ��
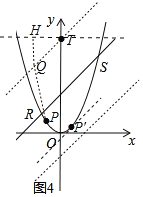
����RSƽ������������ֻ��һ������P����ֱ�߷���Ϊ��y��x+d��
���÷����������߷��������������ã�x2��x��d��0��
����1+4d��0����ã�d����![]() ��
��
��ʱ��x2��x+![]() ��0����ã�x��
��0����ã�x��![]() ��
��
��P����![]() ��
��![]() ������ʱ��P��P����Qȡ����Сֵ��
������ʱ��P��P����Qȡ����Сֵ��
�ڵ���P���ڵ�R���O֮�䣨������R��O��ʱ��
��ͼ4������PQ������Q��QH��ֱ����T��x��ƽ�е�ֱ���ڵ�H��
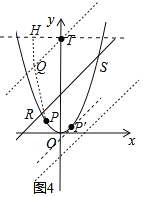
��HQ��![]() QT��
QT��
PQ+![]() QT��PQ+QH��
QT��PQ+QH��
����P���R�غϣ���P��Q��H��һ��ֱ������ֱ��HT��ֱʱ��PQ+![]() QT����Сֵ��
QT����Сֵ��
������СֵΪyT��yR��5��1��4��