题目内容
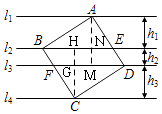
【题目】如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3 . 若h1=2,h2=1,则正方形ABCD的面积为( ) 
A.9
B.10
C.13
D.25
【答案】C
【解析】证明:过A点作AM⊥l3分别交l2、l3于点N、M,过C点作CH⊥l2分别交l2、l3于点H、G,
∵四边形ABCD是正方形,l1∥l2∥l3∥l4,
∴AB=CD,∠ABN+∠HBC=90°,
∵CH⊥l2,
∴∠BCH+∠HBC=90°,
∴∠BCH=∠ABN,
∵∠BCH=∠CDG,
∴∠ABN=∠CDG,
∵∠ANB=∠CGD=90°,
在△ABN和△CDG中,
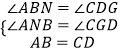 ,
,
∴△ABN≌△CDG(AAS),
∴AN=CG,BE=CH=h2+h3,
即h1=h3=2,BE=2+1=3,
在Rt△ABE中,由勾股定理得:AB2=AE2+BE2=22+32=13,
则正方形ABCD的面积=AB2=13;
故选C.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目