题目内容
如图,已知CA、CB都经过点C,AC是⊙B的切线,⊙B交AB于点D,连接CD并延长交OA于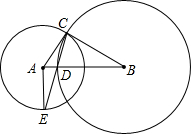 点E,连接AF.
点E,连接AF.
(1)求证:AE⊥AB;
(2)求证:DE•DC=2AD•DB;
(3)如果AE=3,BD=4,求DC的长.
 点E,连接AF.
点E,连接AF.(1)求证:AE⊥AB;
(2)求证:DE•DC=2AD•DB;
(3)如果AE=3,BD=4,求DC的长.
(1)证明:∵AC是⊙B的切线,
∴∠ACB=∠ACD+∠BCD=90°.
∵BC=BD,
∴∠BCD=∠BDC.
∴∠ACD+∠BDC=90°.
∵AC=AE,
∴∠ACD=∠AED.
∵∠ADE=∠BCD,
∴∠AED+∠ADE=90°.
∴∠EAD=90°.
即AE⊥AB.
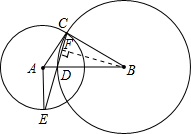
(2)证明:过点B作BF⊥CD于点F,
∵∠ADE=∠BDF,∠EAD=∠BFD,
∴△ADE∽△FDB.
∴
=
.
即DE•FD=AD•DB.
∵DC=2FD,
∴DE•DC=2AD•DB.
(3)∵AE=3,BD=4,
在Rt△ABC中,
(AD+BD)2=AC2+BC2.
即(AD+4)2=32+42解得AD=1,
∴DE=
=
=
.
∵DE•DC=2AD•DB,
即
×DC=2×1×4,
∴DC=
.
∴∠ACB=∠ACD+∠BCD=90°.
∵BC=BD,
∴∠BCD=∠BDC.
∴∠ACD+∠BDC=90°.
∵AC=AE,
∴∠ACD=∠AED.
∵∠ADE=∠BCD,
∴∠AED+∠ADE=90°.
∴∠EAD=90°.
即AE⊥AB.
(2)证明:过点B作BF⊥CD于点F,
∵∠ADE=∠BDF,∠EAD=∠BFD,
∴△ADE∽△FDB.
∴
| DE |
| DB |
| AD |
| FD |
即DE•FD=AD•DB.
∵DC=2FD,
∴DE•DC=2AD•DB.
(3)∵AE=3,BD=4,
在Rt△ABC中,
(AD+BD)2=AC2+BC2.
即(AD+4)2=32+42解得AD=1,
∴DE=
| AE2+AD2 |
| 32+12 |
| 10 |
∵DE•DC=2AD•DB,
即
| 10 |
∴DC=
4
| ||
| 5 |


练习册系列答案
相关题目