��Ŀ����
����Ŀ����һ����ֽƬOABC����ƽ��ֱ������ϵ�У�O��0��0����A��6��0����C��0��3��������Q�ӵ�O������ÿ��1����λ�����ٶ���OC���յ�C�˶����˶�![]() ��ʱ������P�ӵ�A��������ȵ��ٶ���AO���յ�O�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P���˶�ʱ��Ϊt���룩��
��ʱ������P�ӵ�A��������ȵ��ٶ���AO���յ�O�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P���˶�ʱ��Ϊt���룩��
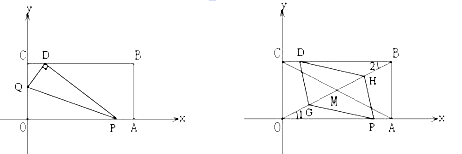
��1�����B�����꣬���ú�t�Ĵ���ʽ��ʾOP��OQ��
��2����t=1ʱ����ͼ1������OPQ��PQ���ۣ���Oǡ������CB���ϵĵ�D�������D�����ꣻ
��3���ڣ�2���������£����ζԽ���AC,BO����M,ȡOM�е�G,BM�е�H����֤��t=1ʱ�ı���DGPH��ƽ���ı�����
���𰸡���1��B��6,3����OP=6��t��OQ=![]() +t����2��D��1,3������3��֤�����̼�����
+t����2��D��1,3������3��֤�����̼�����
��������
�����������1�����ݾ��ε����������B�����꣬���ݶ����������OP��OQ�ij��ȣ���2�������۵�ͼ�ε��������OQ��DQ�ij��ȣ�Ȼ����ݹ��ɶ������CD�ij��ȣ��õ���D�����ꣻ��3������һ��Ա�ƽ������ȵ��ı���Ϊƽ���ı��ν����ж���
�����������1��B��6,3����OP=OA-AP=6-t, OQ=![]() +t��
+t��
��2����t=1ʱ��OP=5��OQ=![]() ,��CQ=3-
,��CQ=3-![]() =
=![]() ��
��
���۵���֪����OPQ�ա�DPQ,
��OQ=DQ=![]()
�ɹ��ɶ���,�ã�CD=1
��D��1,3��
��3�����ı���OABC�Ǿ��Σ�
��OA=BC,
����CD=AP=1��
��BC-CD=OA-AP,��BD=OP,
��OM=MB,GΪOM�е㣬HΪBM�е� ,
��OG=BH,
��OA��BC
���1=��2
����POG����DBH��OG=BH����1=��2��OP=DB
���POG�ա�DBH
���OGP=��BHD��PG=DH
���MGP=��DHM
��PG��DH
����PG=DH
���ı���DGPH��ƽ���ı�����

 �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�