题目内容
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 分钟才乘上缆车,缆车的平均速度为180 米/分钟.设小亮出发x 分钟后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
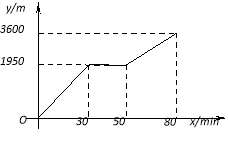
(1)小亮行走的总路程是____________㎝,他途中休息了________min.
(2)①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
【答案】(1)、3600,20;(2)、①、y=55x-800;②、1100m.
【解析】
试题分析:(1)、根据函数图象得出总路程和休息的时间;(2)、①、首先设函数解析式为y=kx+b,将(50,1950)和(80,3600)代入函数解析式得出答案;②、首先求出缆车到达终点所需时间,然后得出小亮行走的时间,然后将求出的时间代入函数解析式得出所行走的路程,从而得出答案.
试题解析:(1)、3600,20.
(2)、①当![]() 时,设y与x的函数关系式为y=kx+b.
时,设y与x的函数关系式为y=kx+b.
根据题意,当x=50时,y=1950;当x=80,y=3600
∴![]() 解得:
解得:![]()
所以,y与x的函数关系式为y=55x-800
②缆车到山顶的路线长为3600÷2=1800(m),
缆车到达终点所需时间为1800÷180=10(min)
小颖到达缆车终点时,小亮行走的时间为10+50=60(min).
把x=60代入y=55x-800,得y=55×60—800=2500.
∴当小颖到达缆车终点时,小亮离缆车终点的路程是3600-2500=1100(m).

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目