题目内容
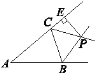
【题目】如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC=________.
【答案】7
【解析】
先过点P作PF⊥AB于G,由于∠ABC和∠ACB的外角平分线BP,CP交于P,
根据角平分线的性质可得PF=PG=PE=2,根据![]() ,可得
,可得![]() ,
,
解得BC=2,再根据△ABC的周长为11,可得AC+AB=11-2=9,继而可得![]() =
=![]() =7.
=7.
如图,
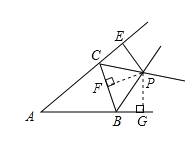
过点P作PF⊥AB于G,
因为∠ABC和∠ACB的外角平分线BP,CP交于P,
所以PF=PG=PE=2,
因为![]() ,
,
所以![]() ,
,
解得BC=2,
因为△ABC的周长为11,
所以AC+AB=11-2=9,
所以![]() ,
,
=![]() ,
,
=7
故答案为:7.

练习册系列答案
相关题目
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.