题目内容
甲乙两地相距400km,一辆轿车从甲地出发,以80km/h的速度匀速驶往乙地.0.5h后,一辆货车从乙地出发匀速驶往甲地.货车出发2.5h后与轿车在途中相遇.此后,两车继续行驶,并各自到达目的地.设轿车行驶的时间为x(h),两车距乙地的距离为y(km).

(1)两车距乙地的距离与x之间的函数关系,在同一坐标系中画出的图象是( )
(2)求货车距乙地的距离y1与x之间的函数关系式.
(3)在甲乙两地间,距乙地300km处有一个加油站,两车在行驶过程中都曾在该加油站加油(加油时间忽略不计).求两车加油的间隔时间是多少?

(1)两车距乙地的距离与x之间的函数关系,在同一坐标系中画出的图象是( )
(2)求货车距乙地的距离y1与x之间的函数关系式.
(3)在甲乙两地间,距乙地300km处有一个加油站,两车在行驶过程中都曾在该加油站加油(加油时间忽略不计).求两车加油的间隔时间是多少?
(1)C;(2)y1=64x-32;(3) h
h
 h
h试题分析:(1)根据“一辆轿车从甲地出发,0.5h后一辆货车从乙地出发匀速驶往甲地.货车出发2.5h后与轿车在途中相遇”即可作出判断;
(2)先求出轿车的行驶时间,再根据待定系数法求得轿车离乙地距离的函数关系式,从而求得D点坐标,设y1=k1x+b1,代入A(0.5,0)、D(3,160)即可根据待定系数法求得结果;
(3)将y=300分别代入求得的两个函数关系式求得对应的x的值,再作差即可求得结果.
(1)两车距乙地的距离与x之间的函数关系,在同一坐标系中画出的图象是C;
(2)轿车行驶时间为400÷80=5(h),设轿车离乙地距离为y2,y2=k2x+b2,
代入(0,400),(5,0)得,k2 =-80,b2=400,
所以y2=-80x+400.代入x=3得,y=160.即D点坐标为(3,160)
设y1=k1x+b1.代入A(0.5,0)、D(3,160)得,k1 =64,b1=-32,
所以y1=64x-32;
(3)将y1=300代入y1=64x-32得x1=
 ,
,将y2=300代入y2=-80x+400得x2=
 ,
,所以x1-x2=
 .
.答:两车加油的间隔时间是
 h.
h.点评:一次函数的应用是初中数学的重点,是中考常见题,一般难度较大,要熟练掌握.

练习册系列答案
相关题目
 ,
, ),B(
),B(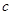 ,
, )在上述一次函数的图象上,且
)在上述一次函数的图象上,且 ,试比较
,试比较 千米)
千米) 吨,总运费为
吨,总运费为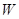 元,试写出
元,试写出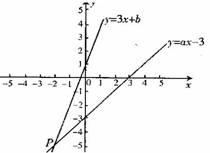
 满足
满足 ,对任意一个
,对任意一个 中的较大值用
中的较大值用 表示,则
表示,则 是正比例函数,则a=___________。
是正比例函数,则a=___________。
 与y=x﹣1的图象的交点坐标为(a,b),则
与y=x﹣1的图象的交点坐标为(a,b),则 ﹣
﹣ 的值为 __________________
的值为 __________________