题目内容
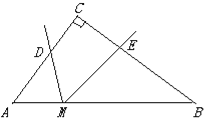
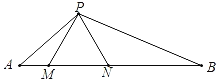
【题目】如图,在△PAB中,M.N是AB上两点,△PMN是等边三角形,∠APM=∠B.
(1)求证:∠A=∠BPN;
(2)求证:MN2=AM·BN;
(3)若AP=![]() ,AM=1,求线段MN,PB的长.
,AM=1,求线段MN,PB的长.
【答案】(1)证明见解析;(2)见解析;(3)MN=2,![]()
【解析】
(1)利用等边三角形的性质可证得∠AMP=∠PNB=![]() ,又∠APM=∠B,可证得△APM∽△PBN,从而证明了∠A=∠BPN;
,又∠APM=∠B,可证得△APM∽△PBN,从而证明了∠A=∠BPN;
(2)由(1)的结论△APM∽△PBN得到![]() ,根据等量代换可证得结论;
,根据等量代换可证得结论;
(3)容易证明△APM∽△ABP,由其对应边成比例及已知,求得![]() ,设MN=x,根据(2)的结论构建方程,求得等边三角形的边长,再根据相似三角形对应边成比例求得最后答案.
,设MN=x,根据(2)的结论构建方程,求得等边三角形的边长,再根据相似三角形对应边成比例求得最后答案.
(1)证明:∵△PMN是等边三角形,
∴∠PMN=∠PNM=60°,
∴∠AMP=∠PNB=120°,
∵∠APM=∠B,
∴△APM∽△PBN,
∠A=∠BPN;
(2)解:∵∠APM=∠B,∠A=∠BPN,
∴△APM∽△PBN,
∴![]() ,即PM·PN=AM·BN,
,即PM·PN=AM·BN,
∵MN=PM=PN,
∴MN 2=AMBN;
(3)解:∵∠A=∠A,∠APM=∠B,
∴△APM∽△ABP,
∴![]() ,
,
∴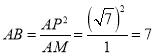 ,
,
设MN=x,则PM=MN=x,BN=6﹣x,
∵MN 2=AMBN,
∴x2=1×(6﹣x),
解得x1=2,x2=﹣3(舍去),
∴PM=MN=2,
∵![]() ,
,
∴![]()

练习册系列答案
相关题目