题目内容
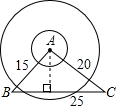 如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
分析:首先利用勾股定理的逆定理判定三角形ABC为直角三角形,然后利用面积相等的方法求得其斜边上的高,大于10不会穿过,否则就穿过.
解答:解:∵AB2+AC2=152+202=252=CB2,
∴△ABC为直角三角形,
作AD⊥BC于D点,
∴S△ABC=
AB•AC=
BC•AD,
即:15×20=25•AD,
解得AD=12,
∵12>10,
∴不会穿过.
∴△ABC为直角三角形,
作AD⊥BC于D点,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即:15×20=25•AD,
解得AD=12,
∵12>10,
∴不会穿过.
点评:本题考查了垂径定理的应用和勾股定理的逆定理的应用,解题的关键是利用面积相等的方法求得其斜边上的高.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 52、如图所示,已知AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有
52、如图所示,已知AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有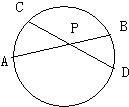 9、如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )
9、如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )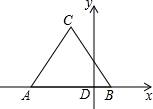 如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).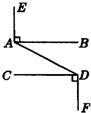 24、如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.
24、如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.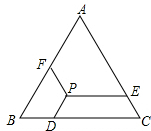 如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=
如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=