题目内容
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 ![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M. 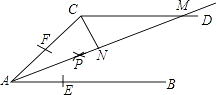
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.
【答案】
(1)解:∵AB∥CD,
∴∠ACD+∠CAB=180°,
又∵∠ACD=114°,
∴∠CAB=66°,
由作法知,AM是∠CAB的平分线,
∴∠MAB= ![]() ∠CAB=33°
∠CAB=33°
(2)证明:∵AM平分∠CAB,
∴∠CAM=∠MAB,
∵AB∥CD,
∴∠MAB=∠CMA,
∴∠CAM=∠CMA,
又∵CN⊥AM,
∴∠ANC=∠MNC,
在△ACN和△MCN中, 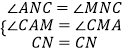 ,
,
∴△ACN≌△MCN(AAS)
【解析】(1)根据AB∥CD,∠ACD=114°,得出∠CAB=66°,再根据AM是∠CAB的平分线,即可得出∠MAB的度数.(2)根据∠CAM=∠MAB,∠MAB=∠CMA,得出∠CAM=∠CMA,再根据CN⊥AD,CN=CN,即可得出△ACN≌△MCN.

练习册系列答案
相关题目