��Ŀ����
��֪��ƽ��ֱ������ϵ�У���O������ԭ�㣬ֱ��y=kx+b��x�ᡢy��ֱ��ڵ�A��B����˫����y=
�ཻ�ڵ�C��D���ҵ�D������Ϊ��1��6����
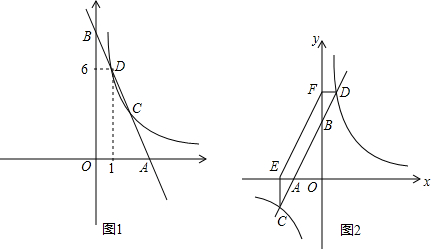
��1����ͼ1������C�ĺ�����Ϊ2ʱ�����C�������
��ֵ��
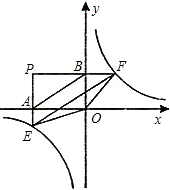
��2����ͼ2������A����x�Ḻ����ʱ������C��x��Ĵ��ߣ�����ΪE������D��y��Ĵ��ߣ�����ΪF������EF��
���жϡ�EFC������͡�EFD������Ƿ���ȣ���˵�����ɣ�
�ڵ�
=2ʱ�����C�������tan��OAB��ֵ��
��3����tan��OAB=
����ֱ��д��
��ֵ��������д������̣�
| m |
| x |
��1����ͼ1������C�ĺ�����Ϊ2ʱ�����C�������
| CD |
| AB |
��2����ͼ2������A����x�Ḻ����ʱ������C��x��Ĵ��ߣ�����ΪE������D��y��Ĵ��ߣ�����ΪF������EF��
���жϡ�EFC������͡�EFD������Ƿ���ȣ���˵�����ɣ�
�ڵ�
| CD |
| AB |
��3����tan��OAB=
| 1 |
| 7 |
| CD |
| AB |

��1����D��1��6����y=
�ϣ�
��m=6����˫���߽���ʽ�� y=
��
��C�������Ϊ2ʱ��������Ϊ3��
��C��2��3����
ֱ��AB����C��2��3����D��1��6������
��
��ã�
��
��ֱ��AB�Ľ���ʽΪy=-3x+9��
��B��0��9����A��3��0����
��AB=3
��
��C��2��3����D��1��6����
��CD=
��
=
��
��2������C��a��b������ab=6��
��S��EFC=
��-a����-b��=
ab=3����S��EFD=
��1��6=3��
��S��EFC=S��EFD��
�ڡ�S��EFC=S��EFD������������ͬ�ף�
���������εĸ���ͬ��
��EF��CD��
��DF��AE��BF��CE��
���ı���DFEA���ı���FBCE����ƽ���ı��Σ�
��CE=BF����FDB=��EAC��
�ڡ�DFB���AEC�У�
��
��
���DFB�ա�AEC��
��AC=BD��
��
=2����CD=2k��AB=k��DB=
��
��
=
��
�ߡ�DFB=��AOB����DBF=ABO��
���DFB����AOB��
��
=
=
=
��
��DF=1��
��OA=2��
��OF=6��
��OB=4��
��tan��OAB=
=2��
��OA=2��OB=4��
��A��-2��0����B��0��4����
��ֱ��AB�Ľ���ʽΪy=2x+4��
������������������ʽ��һ�κ�������ʽ�ɵ�
��
��ã�
��
��
��C��-3��-2����
��3����ͼ2��ֱ����˫���߹�D�㣨1��6��������˫���߷���6=
��
��ã�m=6��
����ֱ�߷��̣�6=k+b��b=6-k��
����ֱ�߷��̱�Ϊy=kx+6-k��
��tan��OAB=
��
��ֱ�߷��̵�б��Ϊ
����k=
��
��b=
��
��ֱ�߷���Ϊy=
x+
��
��A��������-41��0����B��0��
����
�ٽ�ֱ�߷��̴���˫���߷�����
=
x+
�����x=1��-42��
��x=-42��y=-
��
��C��ƽ����x���ֱ�ߣ���D��ƽ����y��ֱ�ߣ���ֱ���ཻ��M��
���AOB����CMD��
��
=
��
CM=1-��-42��=43��AO=41������
=
��
��ͼ1����tan��OAB=
��
��ֱ�߷��̵�б��Ϊ
����k=-
��
��b=
��
��ֱ�߷���Ϊy=-
x+
��
��A��������43��0����B��0��
����
�ٽ�ֱ�߷��̴���˫���߷�����
=-
x+
�����x=1��42��
��x=42��y=
��
�ߡ�AOB����CPD��
��
=
��
CP=42-1=41��AO=43��
��
=
��
����������
��ֵΪ
��
��

| m |
| x |
��m=6����˫���߽���ʽ�� y=
| 6 |
| x |
��C�������Ϊ2ʱ��������Ϊ3��
��C��2��3����
ֱ��AB����C��2��3����D��1��6������
|
��ã�
|
��ֱ��AB�Ľ���ʽΪy=-3x+9��
��B��0��9����A��3��0����
��AB=3
| 10 |
��C��2��3����D��1��6����
��CD=
| 10 |
��
| CD |
| AB |
| 1 |
| 3 |
��2������C��a��b������ab=6��
��S��EFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��S��EFC=S��EFD��
�ڡ�S��EFC=S��EFD������������ͬ�ף�
���������εĸ���ͬ��
��EF��CD��
��DF��AE��BF��CE��
���ı���DFEA���ı���FBCE����ƽ���ı��Σ�
��CE=BF����FDB=��EAC��
�ڡ�DFB���AEC�У�
��
|
���DFB�ա�AEC��
��AC=BD��
��
| CD |
| AB |
| k |
| 2 |
��
| DB |
| AB |
| 1 |
| 2 |
�ߡ�DFB=��AOB����DBF=ABO��
���DFB����AOB��
��
| DF |
| AO |
| DB |
| AB |
| BF |
| BO |
| 1 |
| 2 |
��DF=1��
��OA=2��
��OF=6��
��OB=4��
��tan��OAB=
| BO |
| AO |
��OA=2��OB=4��
��A��-2��0����B��0��4����
��ֱ��AB�Ľ���ʽΪy=2x+4��
������������������ʽ��һ�κ�������ʽ�ɵ�
|
��ã�
|
|
��C��-3��-2����
��3����ͼ2��ֱ����˫���߹�D�㣨1��6��������˫���߷���6=
| m |
| 1 |
��ã�m=6��
����ֱ�߷��̣�6=k+b��b=6-k��
����ֱ�߷��̱�Ϊy=kx+6-k��
��tan��OAB=
| 1 |
| 7 |
��ֱ�߷��̵�б��Ϊ
| 1 |
| 7 |
| 1 |
| 7 |
��b=
| 41 |
| 7 |
��ֱ�߷���Ϊy=
| 1 |
| 7 |
| 41 |
| 7 |
��A��������-41��0����B��0��
| 41 |
| 7 |
�ٽ�ֱ�߷��̴���˫���߷�����
| 6 |
| x |
| 1 |
| 7 |
| 41 |
| 7 |
��x=-42��y=-
| 1 |
| 7 |
��C��ƽ����x���ֱ�ߣ���D��ƽ����y��ֱ�ߣ���ֱ���ཻ��M��
���AOB����CMD��
��
| CD |
| AB |
| CM |
| AO |
CM=1-��-42��=43��AO=41������
| CD |
| AB |
| 43 |
| 41 |
��ͼ1����tan��OAB=
| 1 |
| 7 |
��ֱ�߷��̵�б��Ϊ
| 1 |
| 7 |
| 1 |
| 7 |
��b=
| 43 |
| 7 |
��ֱ�߷���Ϊy=-
| 1 |
| 7 |
| 43 |
| 7 |
��A��������43��0����B��0��
| 43 |
| 7 |
�ٽ�ֱ�߷��̴���˫���߷�����
| 6 |
| x |
| 1 |
| 7 |
| 43 |
| 7 |
��x=42��y=
| 1 |
| 7 |
�ߡ�AOB����CPD��
��
| CD |
| AB |
| CP |
| AO |
CP=42-1=41��AO=43��
��
| CD |
| AB |
| 41 |
| 43 |
����������
| CD |
| AB |
| 43 |
| 41 |
| 41 |
| 43 |


��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
�����Ŀ

 ������OAB��O��˳ʱ����ת30���ǡ��A����˫����y=
������OAB��O��˳ʱ����ת30���ǡ��A����˫����y=