题目内容
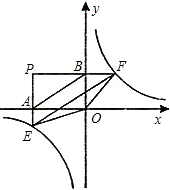
如图,过点P(-4,3)作x轴,y轴的垂线,分别交x轴,y轴于A、B两点,交双曲线y=
(k≥2)于E、F两点.
(1)点E的坐标是______,点F的坐标是______;(均用含k的式子表示)
(2)判断EF与AB的位置关系,并证明你的结论;
(3)记S=S△PEF-S△OEF,S是否有最小值?若有,求出其最小值;若没有,请你说明理由.
| k |
| x |
(1)点E的坐标是______,点F的坐标是______;(均用含k的式子表示)
(2)判断EF与AB的位置关系,并证明你的结论;
(3)记S=S△PEF-S△OEF,S是否有最小值?若有,求出其最小值;若没有,请你说明理由.

(1)E(-4,-
),F(
,3);
(2)结论EF∥AB.理由如下:
∵P(-4,3),
∴E(-4,-
),F(
,3),
即得PE=3+
,PF=
+4,
在Rt△PAB中,tan∠PAB=
=
,
在Rt△PEF中,tan∠PEF=
=
=
,
∴tan∠PAB=tan∠PEF,
∴∠PAB=∠PEF,
∴EF∥AB;
(3)S有最小值.理由如下:
分别过点E、F作PF、PE的平行线,交点为P′.
由(2)知P′(
,-
)
∵四边形PEP′F是矩形,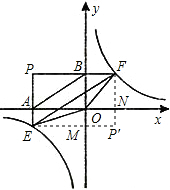
∴S△P′EF=S△PEF,
∴S=S△PEF-S△OEF
=S△P′EF-S△OEF
=S△OME+S矩形OMP′N+S△ONF
=
+
+
=
+k
=
(k+6)2-3,
又∵k≥2,此时S的值随k值增大而增大,
∴当k=2时,S最小=
.
∴S的最小值是
.
故答案为:(1)(-4,-
),(
,3).
| k |
| 4 |
| k |
| 3 |
(2)结论EF∥AB.理由如下:
∵P(-4,3),
∴E(-4,-
| k |
| 4 |
| k |
| 3 |
即得PE=3+
| k |
| 4 |
| k |
| 3 |
在Rt△PAB中,tan∠PAB=
| PB |
| PA |
| 4 |
| 3 |
在Rt△PEF中,tan∠PEF=
| PF |
| PE |
| ||
3+
|
| 4 |
| 3 |
∴tan∠PAB=tan∠PEF,
∴∠PAB=∠PEF,
∴EF∥AB;
(3)S有最小值.理由如下:
分别过点E、F作PF、PE的平行线,交点为P′.
由(2)知P′(
| k |
| 3 |
| k |
| 4 |
∵四边形PEP′F是矩形,

∴S△P′EF=S△PEF,
∴S=S△PEF-S△OEF
=S△P′EF-S△OEF
=S△OME+S矩形OMP′N+S△ONF
=
| k |
| 2 |
| k2 |
| 12 |
| k |
| 2 |
=
| k2 |
| 12 |
=
| 1 |
| 12 |
又∵k≥2,此时S的值随k值增大而增大,
∴当k=2时,S最小=
| 7 |
| 3 |
∴S的最小值是
| 7 |
| 3 |
故答案为:(1)(-4,-
| k |
| 4 |
| k |
| 3 |

练习册系列答案
相关题目




 不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.
不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.

