题目内容
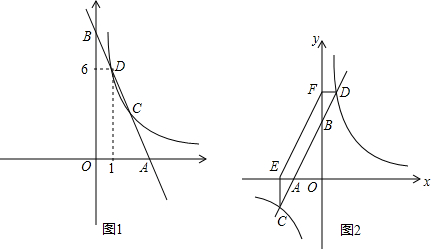
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.

| k |
| x |
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.

(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=
(x>0)的图象上,
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-
,0),B(0,b).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=
(x>0)的图象上,
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=
| k |
| x |
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-
| b |
| 2 |
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=
| k |
| x |
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目




 图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上
图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上