题目内容
已知函数y1=x,y2=x2+bx+c,α,β为方程y1-y2=0的两个根,点M(t,T)在函数y2的图象上。
(Ⅰ)若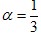 ,
,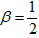 ,求函数y2的解析式;
,求函数y2的解析式;
(Ⅱ)在(Ⅰ)的条件下,若函数y1与y2的图象的两个交点为A,B,当△ABM的面积为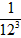 时,求t的值;
时,求t的值;
(Ⅲ)若0<α<β<1,当0<t<1时,试确定T,α,β三者之间的大小关系,并说明理由。
(Ⅰ)若
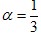 ,
,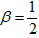 ,求函数y2的解析式;
,求函数y2的解析式;(Ⅱ)在(Ⅰ)的条件下,若函数y1与y2的图象的两个交点为A,B,当△ABM的面积为
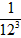 时,求t的值;
时,求t的值;(Ⅲ)若0<α<β<1,当0<t<1时,试确定T,α,β三者之间的大小关系,并说明理由。
解:(I)∵y1=x,y2=x2+bx+c,y1-y2=0,
∴x2+(b-1)x+c=0,
将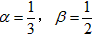 分别代入x2+(b-1)x+c=0,得
分别代入x2+(b-1)x+c=0,得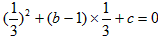 ,
,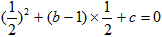 ,
,
解得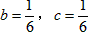 ,
,
∴函数y2的解析式为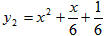 ;
;
(Ⅱ)由已知,得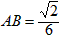 ,设△ABM的边AB上的高为h,
,设△ABM的边AB上的高为h,
∴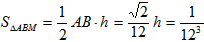 ,即
,即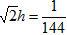 ,
,
根据题意,|t-T|=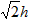 ,
,
由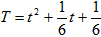 得
得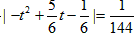 ,
,
当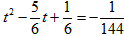 ,解得
,解得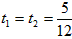 ,
,
当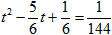 ,解得
,解得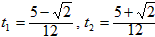 ,
,
∴t的值为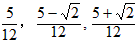 ;
;
(Ⅲ)由已知,得
α=α2+bα+c,β=β2+bβ+c,T=t2+bt+c,
∴T-α=(t-α)(t+α+b)
T-β=(t-β)(t+β+b),
α-β=(α2+bα+c)-(β2+bβ+c),
化简得(α-β)(α+β+b-1)=0
由0<α<β<1,得α-β≠0,
α+β+b-1=0,
有α+b=1-β>0,β+b=1-α>0,
又0<t<1,∴t+α+b>0,t+β+b>0,
∴当0<t≤α时,T≤α<β;
当α<t≤β时,α<T≤β;
当β<t<1时,α<β<T。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数y1=x-1和
已知函数y1=x-1和 已知函数y1=x+2,y2=-2x+8
已知函数y1=x+2,y2=-2x+8 如图,已知函数y1=ax+b和y2=kx的图象交于点P,根据图象可得,当y1<y2时,x的取值范围是
如图,已知函数y1=ax+b和y2=kx的图象交于点P,根据图象可得,当y1<y2时,x的取值范围是