题目内容
 已知函数y1=x+2,y2=-2x+8
已知函数y1=x+2,y2=-2x+8(1)在同一坐标系中画出两个函数的图象;
(2)求两条直线的交点坐标.
(3)求两条直线与x轴围成的三角形面积
(4)观察图象求出:
A、当x为何值时,有y2>0;
B、当x为何值时,有y1、y2同时大于0.
分析:(1)分别求得两个函数与坐标轴的交点坐标即可求得两函数的图象;
(2)令y1=y2即可得到x+2=-2x+8求得x值后即可得到交点坐标的横坐标,代入原函数的解析式求得y值即可求得交点坐标的纵坐标;
(3)分别求得两条直线与x轴的交点坐标后即可求得两条直线在x轴上截的线段的长,然后乘以交点坐标的纵坐标的绝对值即可求得面积;
(4)直接观察图象即可得到答案;
(2)令y1=y2即可得到x+2=-2x+8求得x值后即可得到交点坐标的横坐标,代入原函数的解析式求得y值即可求得交点坐标的纵坐标;
(3)分别求得两条直线与x轴的交点坐标后即可求得两条直线在x轴上截的线段的长,然后乘以交点坐标的纵坐标的绝对值即可求得面积;
(4)直接观察图象即可得到答案;
解答:解:(1)令y1=x+2=0,解得:x=-2,
将x=0代y1=x+2=2,
故y1=x+2与x轴交与点(-2,0),与y轴交与点(0,2)
令y2=-2x+8=0得x=4,
令x=0得y2=-2x+8=8,
故y2=-2x+8与x轴交与点(4,0)与y轴交与点(0,8)
故图象为:
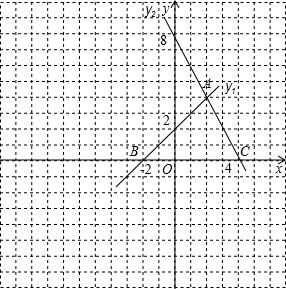
(2)令y1=y2即可得到x+2=-2x+8,
解得:x=2,
将x=2代入y1=x+2=4,
故交点A坐标为(2,4);
(3)如图:S△ABC=
×6×4=12;
(4)A、∵观察图象知:当x<4时候,函数y2的图象位于x州的上方,
∴当x<4时,y2>0;
B、观察图象知:当-2<x<4时候,函数y1、y2的图象均位于x州的上方,
∴当-2<x<4时,y1、y2同时大于0.;
将x=0代y1=x+2=2,
故y1=x+2与x轴交与点(-2,0),与y轴交与点(0,2)
令y2=-2x+8=0得x=4,
令x=0得y2=-2x+8=8,
故y2=-2x+8与x轴交与点(4,0)与y轴交与点(0,8)
故图象为:

(2)令y1=y2即可得到x+2=-2x+8,
解得:x=2,
将x=2代入y1=x+2=4,
故交点A坐标为(2,4);
(3)如图:S△ABC=
| 1 |
| 2 |
(4)A、∵观察图象知:当x<4时候,函数y2的图象位于x州的上方,
∴当x<4时,y2>0;
B、观察图象知:当-2<x<4时候,函数y1、y2的图象均位于x州的上方,
∴当-2<x<4时,y1、y2同时大于0.;
点评:本题考查了反比例函数的图象,解题的关键是利用两点法作出函数的图象,然后确定各题的答案.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 已知函数y1=x-1和
已知函数y1=x-1和 如图,已知函数y1=ax+b和y2=kx的图象交于点P,根据图象可得,当y1<y2时,x的取值范围是
如图,已知函数y1=ax+b和y2=kx的图象交于点P,根据图象可得,当y1<y2时,x的取值范围是