题目内容
 已知函数y1=x-1和y2=
已知函数y1=x-1和y2=| 6 | x |
(1)在所给的坐标系中画出这两个函数的图象.
(2)求这两个函数图象的交点坐标.
(3)观察图象,当x在什么范围时,y1>y2?
分析:(1)画图的步骤:列表,描点,连线.需注意函数y1的自变量取值范围是:全体实数;函数y2的自变量取值范围是:x≠0.
(2)交点都适合这两个函数解析式,应让这两个函数解析式组成方程组求解即可.
(3)从交点入手,看在交点的哪一边一次函数的函数值大于反比例函数的函数值.
(2)交点都适合这两个函数解析式,应让这两个函数解析式组成方程组求解即可.
(3)从交点入手,看在交点的哪一边一次函数的函数值大于反比例函数的函数值.
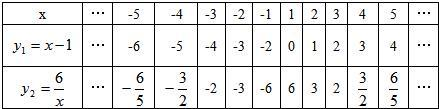
解答:解:(1)函数y1的自变量取值范围是:全体实数;函数y2的自变量取值范围是:x≠0.列表可得:
(2)联立解析式:
,
解得:
,
.
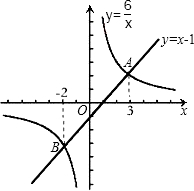
∴两函数的交点坐标分别为A(-2,-3);B(3,2);
(3)由图象观察可得:当-2<x<0或x>3时,y1>y2.

(2)联立解析式:
|
解得:
|
|
∴两函数的交点坐标分别为A(-2,-3);B(3,2);
(3)由图象观察可得:当-2<x<0或x>3时,y1>y2.

点评:本题考查了反比例函数和一次函数的图象.无论是求自变量的取值范围还是函数值的取值范围,都应该从交点入手思考.

练习册系列答案
相关题目
 已知函数y1=x+2,y2=-2x+8
已知函数y1=x+2,y2=-2x+8 如图,已知函数y1=ax+b和y2=kx的图象交于点P,根据图象可得,当y1<y2时,x的取值范围是
如图,已知函数y1=ax+b和y2=kx的图象交于点P,根据图象可得,当y1<y2时,x的取值范围是