Question

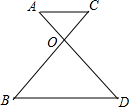如图，已知AC∥BD，OA=OC，则下列结论不一定成立的是（　　）

• A．∠A=∠B
• B．∠B=∠D
• C．AD=BC
• D．OA=

  1

  2

  OB

Answer 1

分析：根据等边对等角的性质可得∠A=∠C，再根据两直线平行，内错角相等可得∠A=∠D，∠C=∠B，然后求出∠A=∠B=∠C=∠D，再根据等角对等边的性质可得OB=OD，从而求出AD=BC．

解答：解：∵OA=OC，
∴∠A=∠C，
∵AC∥BD，
∴∠A=∠D，∠C=∠B，
∴∠A=∠B=∠C=∠D，故A、B选项正确；
∴OA+OD=OB+OC，
即AD=BC，故C选项正确；
只有OA=

1

2

OD时，OA=

1

2

OB，无法说明OA=

1

2

OD，故D选项错误．
故选D．

点评：本题考查了两直线平行，内错角相等的性质，等边对等角，等角对等边的性质，是基础题．