题目内容
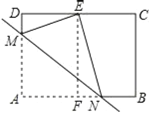
【题目】如图,已知矩形ABCD,E,F分别是边AB,CD的中点,M,N分别是边AD,AB上两点,将△AMN沿MN对折,使点A落在点E上.若AB=a,BC=b,且N是FB的中点,则![]() 的值为____.
的值为____.
【答案】![]() .
.
【解析】
由题意可证四边形ADEF是矩形,可得AD=EF=b,∠EFB=90°,由折叠性质可得AN=EN=![]() a,由勾股定理可求解.
a,由勾股定理可求解.
解:∵四边形ABCD是矩形
∴AB=CD,AB∥CD,∠A=90°
∵E,F分别是边AB,CD的中点,N是FB的中点,
∴DE=AF=BF=![]() AB=
AB=![]() a,FN=
a,FN=![]() AB=
AB=![]() a,
a,
∴AN=AF+FN=![]() a
a
∵AF=DE,DC∥AB,∠A=90°
∴四边形ADEF是矩形
∴AD=EF=b,∠EFB=90°
∵将△AMN沿MN对折,使点A落在点E上
∴AN=EN=![]() a,
a,
在Rt△EFN中,EN2=EF2+FN2,
∴![]() a2=b2+
a2=b2+![]() a2,
a2,
∴b=![]() a
a
∴![]()
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某市教育主管部门为了解学生的作业量情况,随机抽取了几所中学八年级的部分学生进行了一次调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图、表中所提供的信息解答下列问题:
(1)本次共抽取了 名学生进行调查;
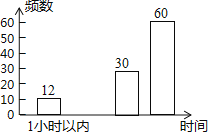
(2)x= ,y= ,补全条形统计图;
(3)若这几所中学八年级的学生共有3200人,请估计做作业时间在2小时以上的学生人数是多少?
(4)由图表可知,这次被调查的八年级学生的作业时间的中位数一定落在1.5小时﹣2小时这一时段内,你认为这种判断正确吗?(不需要说明理由)
写作业时间 | 频数 | 频率 |
1小时以内 | 12 | 0.1 |
1﹣1.5 | x | 0.15 |
1.5﹣2 | 30 | 0.25 |
2小时以上 | 60 | y |
【题目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .现要把这些肥料全部运往
.现要把这些肥料全部运往![]() 、
、![]() 两乡,
两乡,![]() 乡需要肥料240t,
乡需要肥料240t,![]() 乡需要肥料
乡需要肥料![]() ,其运往
,其运往![]() 、
、![]() 两乡的运费如下表:
两乡的运费如下表:
两城/两乡 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() ,从
,从![]() 城运往两乡的总运费为
城运往两乡的总运费为元,从
![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元
元
(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较![]() 、
、![]() 两城总运费的大小;
两城总运费的大小;
(3)若![]() 城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?