题目内容
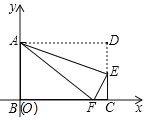
【题目】如图,以矩形ABCD的相邻边建立直角坐标系,AB=3,BC=5.点E是边CD上一点,将△ADE沿着AE翻折,点D恰好落在BC边上,记为F.
(1)求折痕AE所在直线的函数解析式______;
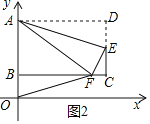
(2)若把翻折后的矩形沿y轴正半轴向上平移m个单位,连结OF,若△OAF是等腰三角形,则m的值是______,
【答案】y=-![]() x+3 3或2或
x+3 3或2或![]() .
.
【解析】
(1)根据四边形ABCD是矩形以及由折叠对称性得出AF=AD=5,EF=DE,进而求出BF的长,即可得出E点的坐标,进而得出AE所在直线的解析式;
(2)分三种情况讨论:若AO=AF,OF=FA,AO=OF,利用勾股定理求出即可.
解:(1)∵四边形ABCD是矩形,
∴AD=CB=5,AB=DC=3,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=5,EF=DE,
在Rt△ABF中,BF=![]() =4,
=4,
∴CF=1,
设EC=x,则EF=3-x,
在Rt△ECF中,12+x2=(3-x)2,
解得:x=![]() ,
,
∴E点坐标为:(5,![]() ),
),
∴设AE所在直线解析式为:y=ax+b,
则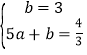
解得: 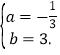
∴AE所在直线解析式为:y=![]() x+3;
x+3;
故答案为:y=![]() x+3;
x+3;
(2)分三种情况讨论:
若AO=AF=BC=5,
∴BO=AO-AB=2,
∴m=2;
若OF=FA,则AB=OB=3,
∴m=3,
若AO=OF,
在Rt△OBF中,AO2=OB2+BF2=m2+16,
∴(m+3)2=m2+16,
解得:m=![]() ,
,
综上所述,若△OAF是等腰三角形,m的值为3或2或![]() .
.
故答案为:3或2或![]() .
.

【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
优等品的频数m | 48 | 95 | 188 | x | 948 | 1426 | 1898 |
优等品的频率 | 0.960 | y | 0.940 | 0.944 | z | 0.951 | 0.949 |
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).