Question

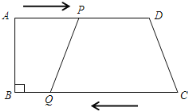
【题目】在矩形ABCD中，AB＝3，BC＝2，以点A为旋转中心，逆时针旋转矩形ABCD，旋转角为α（0°＜α＜180°），得到矩形AEFG，点B、点C、点D的对应点分别为点E、点F、点G．

（1）如图①，当点E落在DC边上时，直写出线段EC的长度为　 　；

（2）如图②，当点E落在线段CF上时，AE与DC相交于点H，连接AC，

①求证：△ACD≌△CAE；

②直接写出线段DH的长度为　　 ．

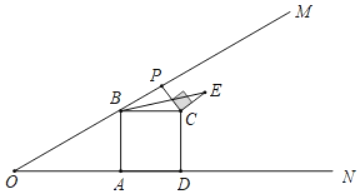
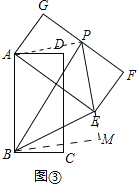
（3）如图③设点P为边FG的中点，连接PB，PE，在矩形ABCD旋转过程中，△BEP的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．

Answer 1

【答案】(1) (2) ①证明见解析，②；（3）存在，.

【解析】

(1)根据勾股定理求出DE的长度，即可求解.

（2）①根据HL即可判定三角形全等.

②设 在Rt△ADH中根据勾股定理即可求解.

（3）如图③中，连接PA，作BM⊥PE交PE的延长线于M．根据题意可得：PF＝PG=，

则PA＝PE＝，S△PBE＝PEBM＝BM，当BM的值最大时，△PBE的面积最大，求出BM的最大值即可.

(1)

故答案为：

(2) ①证明：如图②中，

∵当点E落在线段CF上，

∴∠AEC＝∠ADC＝90°，

在Rt△ADC和Rt△AEC中，

∴Rt△ACD≌Rt△CAE（HL）；

②

（3）存在．

理由：如图③中，连接PA，作BM⊥PE交PE的延长线于M．

由题意：PF＝PG=，

∵AG＝EF＝2，∠G＝∠F＝90°，∴PA＝PE＝，

∴S△PBE＝PEBM＝BM，

∴当BM的值最大时，△PBE的面积最大，

∵BM≤PB，PB≤AB+PA，

∴PB≤3+img src="http://thumb.zyjl.cn/questionBank/Upload/2020/06/09/06/2d6c918a/SYS202006090604111882361116_DA/SYS202006090604111882361116_DA.007.png" width="9" height="33" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=，∴BM≤，∴BM的最大值为，此时点B、A、P三点共线，

∴△PBE的面积的最大值为．