题目内容
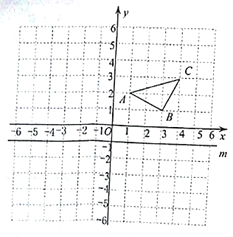
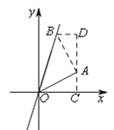
【题目】在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式为___________.
【答案】![]() 或
或![]()
【解析】由直线y=kx与线段OA的夹角是45°可知,本题有两种情况:一种是直线y=kx在线段OA的上方(即直线y=kx的图象经过第一、三象限);另一种是直线y=kx在线段OA的下方(直线y=kx的图象经过第二、四象限).再通过以直线y=kx与OA构造等腰直角三角形即可进行求解.
解:有两种情况:
①当直线y=kx在线段OA的上方时(即直线y=kx的图象经过第一、三象限),
如图所示,过点A作AB⊥OA,交直线y=kx于点B,过点A作平行于y轴的直线交x轴于点C,过点B作BD⊥AC,垂足为D.
∵AB⊥OA
∴∠OAB=90°
∵∠BOA=45°
∴△OAB等腰直角三角形
∴OA=OB
∵∠OAC+∠BAD =90°, ∠OAC+∠AOC =90°
∴∠BAD=∠AOC
又∵∠D=∠ACO =90°
∴△OCA≌△BAD
∴AD=OC,BD=AC
∵A(2,1),
∴OC=2,AC=1
∴AD=OC=2,BD=AC=1
∴D点坐标为(2,3) ∴B点坐标为(1,3)
∴此时正比例函数表达式为:y=3x
②当直线y=kx在线段OA的下方时(即直线y=kx的图象经过第二、四象限):
过点A作AB⊥OA,交直线y=kx于点B,过点A作平行于x轴的直线交y轴于点C,过点B作BD⊥AC .

则由①可知:
∴△OCA≌△BAD
∴AD=OC,BD=AC
∵A(2,1),
∴OC=1,AC=2
∴AD=OC=1,BD=AC=2
∴D点坐标为(3,1)
∴B点坐标为(3,﹣1)
∴此时正比例函数表达式为:y=![]() x
x
∴正比例函数表达式为:![]() 或
或![]()

练习册系列答案
相关题目