Question

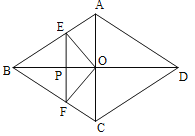
【题目】已知如图，在⊙O中，AB，CD是直径，BE是切线，B为切点，

连接AD，BC，BD．

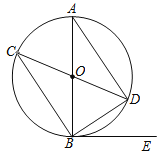
（1）求证：△ABD≌△CDB；

（2）若∠DBE=35°，求∠ADC的度数．

Answer 1

【答案】（1）证明见解析；（2）35°

【解析】（1）根据直径所对的圆周角为直角，可得出∠CBD=∠ADB=90°，再根据同弧所对的圆周角相等，可得∠A＝∠C，利用AAS即可证明全等；（2）根据切线性质可得∠ABE＝90°，结合已知条件∠DBE＝35°，∠CBD＝90°可求出∠CBA的度数，再根据同弧所对的圆周角相等即可得到∠ADC的度数．

（1）证明：∵在⊙O中，AB，CD是直径，

∴∠ADB＝∠CBD＝90°，

AB＝CD．

∵∠A＝∠C，

∴△ABD≌△CDB．

（2）∵BE是切线，B为切点，AB是直径，

∴∠ABE＝90°．

∵∠DBE＝35°，∴∠ABD＝55°．

∵∠CBD＝90°，∴∠CBA＝35°

∴∠ADC＝∠CBA＝35°．