题目内容
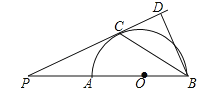
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() 经过点
经过点![]() 过点
过点![]() 作
作![]() 的切线
的切线![]() 点
点![]() 是
是![]() 上不与点
上不与点![]() 重合的一个动点,连接
重合的一个动点,连接![]() .
.
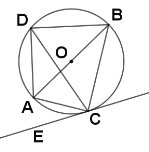
![]() 求证:
求证:![]() ;
;
![]() 填空:
填空:
![]() 当
当![]() _ 时,
_ 时,![]() 为等腰直角三角形:
为等腰直角三角形:
![]() 当
当![]() 时,四边形
时,四边形![]() 为菱形.
为菱形.
【答案】![]() 见解析;
见解析;![]() ①45°②120°
①45°②120°
【解析】
(1)连接OC.根据等腰三角形的性质得到∠OCB=∠OBC,根据平行线的性质得到∠ACB=90°.再根据切线的性质定理及圆周角定理即可得到结论;
(2)①根据圆的对称性由BD=AD可得弧BD=弧AD,再由圆周角定理得∠DCB=∠DCA,进而得解;
②由菱形可得OD=AD,结合OD=OA,证得△OAD为等边三角形,则∠OAD=60°,最后根据圆周角定理即可得解.
解:![]() 如图,连接
如图,连接![]()
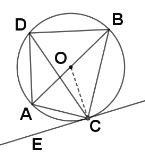
![]()
![]()
![]() 为
为![]() 的直径,
的直径,
![]()
![]() ,
,
![]() 是
是![]() 的切线,
的切线,
![]()
![]()
![]()
![]()
![]()
(2)①∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴AD=DB,
∴弧AD=弧DB,
∴∠ACD=∠DCB=![]() ∠ACB,
∠ACB,
∵∠ACB=90°,
∴∠DCB=45°,
②∵四边形![]() 为菱形,
为菱形,
∴OD=AD,
又∵OD=OA,
∴OD=OA=AD,
∴△AOD为等边三角形,
∴∠OAD=60°,
∵∠OAD=![]() ∠DOB,
∠DOB,
∴∠DOB=120°.

练习册系列答案
相关题目
【题目】小字计划在某外卖网站点如下表所示的菜品,已知每份订单的配送费为3元,商家为了促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元,如果小宇在购买下表中所有菜品时,采取适当的下订单方式,那么他点餐的总费用最低可为___元.
菜品 | 单价(含包装费) | 数量 |
| 30元 | 1 |
| 12元 | 1 |
| 30元 | 1 |
| 12元 | 1 |
| 3元 | 2 |