题目内容
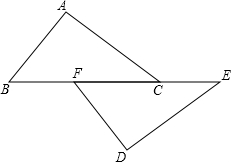
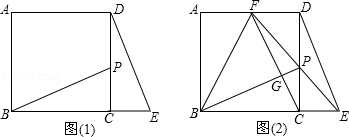
如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,
求证:AC=DF.
求证:AC=DF.

证明:∵AB∥ED,∴∠B=∠E。
∵AC∥FD,∴∠ACB=∠DFE。
∵FB=CE,∴BC=EF。
∴△ABC≌△DEF(ASA)。∴AC=DF。
∵AC∥FD,∴∠ACB=∠DFE。
∵FB=CE,∴BC=EF。
∴△ABC≌△DEF(ASA)。∴AC=DF。
由已知和平行线的性质易根据ASA证明△ABC≌△DEF,从而根据全等三角形对应边相等的性质得出结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
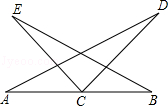
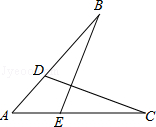
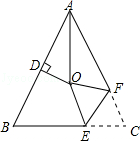
 B.
B. C.
C. D.
D.