Question

如图，在平行四边形ABCD中，AB＞CD，按以下步骤作图：以A为圆心，小于AD的长为半径画弧，分别交AB、CD于E、F；再分别以E、F为圆心，大于EF的长半径画弧，两弧交于点G；作射线AG交CD于点H。则下列结论：
①AG平分∠DAB，②CH＝DH，③△ADH是等腰三角形，④S_△ADH＝S_{四边形ABCH}。
其中正确的有

A．①②③             B．①③④             C．②④             D．①③

Answer 1

D

试题分析：①如图，连接EG，FG，

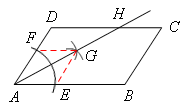
由作图可得，AE=AF，EG=FG，
又∵AG=AG，∴△AEG≌△AFG（SSS）。
∴∠EAG=∠FAG，即AG平分∠DAB。故结论①正确。
③∵在平行四边形ABCD中，DC∥AB，∴∠HAB=DHA。
由①∠HAB=∠HAD，∴∠HAD=DHA。∴DA=DH，即△ADH是等腰三角形。故结论③正确。
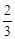②若CH＝DH，由③可得AB=DC＝AD，与已知AB＞CD条件不符。故结论②错误。
④若S_△ADH＝S_{四边形ABCH}，由③可得AB=DC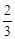＝AD，与已知AB＞CD条件不符。故结论②错误。
综上所述，正确的有①③。故选D。