题目内容
【题目】如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( ).
A.![]() cm
cm
B.9 cm
C.![]() cm
cm
D.![]() cm
cm
【答案】C
【解析】如图,圆心为A,设大正方形的边长为2x,圆的半径为R,
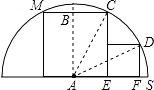
∵正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,
∴AE=BC=x,CE=2x;
∵小正方形的面积为16cm2,
∴小正方形的边长EF=DF=4,
由勾股定理得,R2=AE2+CE2=AF2+DF2,
即x2+4x2=(x+4)2+42,
解得,x=4,
∴R=4 ![]() cm,
cm,
故答案为:C.
观察图形可知正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,因此设大正方形的边长为2x,圆的半径为R,根据小正方形的面积可求出EF=DF=4,再根据R2=AE2+CE2=AF2+DF2,建立关于x的方程,求解即可得出圆的半径长。

练习册系列答案
相关题目