题目内容
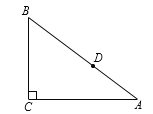
【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为____.
【答案】![]() 、
、 ![]() 、
、 ![]()
【解析】
根据直线平分三角形周长得出线段的和差关系,再通过四种情形下的相似三角形的性质计算线段的长.
解:设过点D的直线与△ABC的另一个交点为E,
∵AC=4,BC=3,∴AB=![]() =5
=5
设AD=x,BD=5-x,
∵DE平分△ABC周长,∴周长的一半为(3+4+5)÷2=6,
分四种情况讨论:
①△BED∽△BCA,如图1,BE=1+x
∴![]() ,即:
,即:![]() ,
,
解得x=![]() ,
,
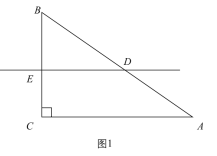
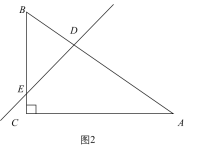
②△BDE∽△BCA,如图2,BE=1+x
∴![]() ,即:
,即:![]() ,
,
解得:x=![]() ,
,
BE=![]() >BC,不符合题意.
>BC,不符合题意.
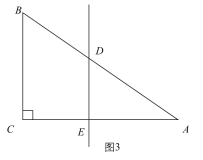
③△ADE∽△ABC,如图3,AE=6-x
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
④△BDE∽△BCA,如图4,AE=6-x
∴![]() ,即:
,即:![]() ,
,
解得:x=![]() ,
,

综上:AD的长为![]() 、
、 ![]() 、
、 ![]() .
.

练习册系列答案
相关题目
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
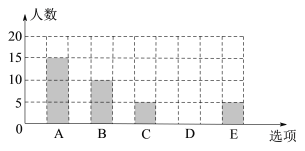
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.