题目内容
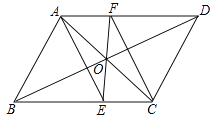
【题目】如图，ABCD的对角线AC、BD交于点O，EF过点O且与BC、AD分别交于点E、F．试猜想线段AE、CF的关系，并说明理由．
【答案】AE与CF的关系是平行且相等．
【解析】
试题分析：先猜出AE与CF的关系，然后说明理由即可，由题意可以推出四边形AECF是平行四边形，从而可以推出AE与CF的关系．
试题解析：AE与CF的关系是平行且相等．
理由：∵在，ABCD中，∴OA=OC，AF∥EC，∴∠OAF=∠OCE，在△OAF和△OCE中，∵∠OAF=∠OCE，OA=OCA，∠EOC=∠FOA，∴△OAF≌△OCE（ASA），∴AF=CE，又∵AF∥CE，∴四边形AECF是平行四边形，∴AE∥CF且AE=CF，即AE与CF的关系是平行且相等．
练习册系列答案
阅读快车系列答案
相关题目
