题目内容
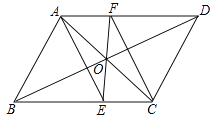
【题目】如图，正方形ABCD，点P为对角线AC上一个动点，Q为CD边上一点，且
（1）求证：PB=PQ；
（2）若BC+CQ=8，求四边形VCQP的面积；
（3）设AP=x，ABCD的面积为y，且CQ=2，求y与x的函数关系式.
【答案】（1）证明见解析；（2）16；（3）y=
【解析】试题分析：（1）如图1中，作PE⊥BC于E，PF⊥CD于F．只要证明△PEB≌△PFQ即可解决问题；
（2）只要证明S四边形BCQP=S四边形CEPF即可解决问题；
（3）如图2，过P做EF∥AD分别交AB和CD于E、F．易知AE=PE=
x，由△BPE≌△PQF，推出EP=AE=QF=x，由BE=CF=2+x，推出AB=2+x+x=2+
x，由此即可解决问题；
试题解析：(1)证明：如图1中，作PE⊥BC于E，PF⊥CD于F.
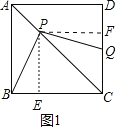
∵四边形ABCD是正方形，
∴∠ACD=∠ACB，
∵PE⊥BC于E，PF⊥CD于F，
∴PE=PF，
∵∠PEC=∠PFC=∠ECF=90°，
∴四边形PECF是矩形，
∵PE=PF，
∴四边形PECF是正方形，
∴∠EPF=∠BPQ=90°,
∴∠BPE=∠QPF,
∵∠PEB=∠PFQ=90°，
∴△PEB≌△PFQ，
∴PB=PQ.
(2)如图1中,由(1)可知△BPE≌△PQF，四边形PECF是正方形，
∴BE=FQ,CE=CF,S△BPE=S△PQF，
∵BC+CQ=8，
∴EC+FC=BC+CQ=8，
∴CE=CF=4,
又∵S△BPE=S△PQF，
∴S四边形BCQP=S四边形CEPF=16.
(3)如图2,过P做EF∥AD分别交AB和CD于E. F.
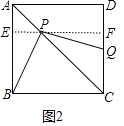
∵AP=x，
∴AE=PE=x，
∵△BPE≌△PQF，
∴EP=AE=QF=x，
∵BE=CF=2+x，
∴AB=2+x+x=2+x，
∴y=(2+x)2=2x2+4x+4.
