题目内容
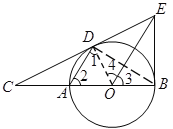
【题目】如图,![]() 是⊙
是⊙![]() 上一点,点
上一点,点![]() 在直径
在直径![]() 的延长线上,且
的延长线上,且![]() 是⊙
是⊙![]() 的切线,
的切线,![]() ∥
∥![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连结
,连结![]() .
.
(1) 求证:![]() 是⊙
是⊙![]() 的切线.
的切线.
(2) 若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径.
的半径.

【答案】(1)详见解析;(2)1
【解析】
(1)连接OD,由平行线的性质和等腰三角形的性质得出![]() ,证明△OBE≌△ODE得出
,证明△OBE≌△ODE得出![]() ,即可得出结论;
,即可得出结论;
(2)连接BD,设⊙O的半径为r,由圆周角定理得出∠ADB=90![]() ,在Rt△ADB和Rt△ODE中,由三角函数得出
,在Rt△ADB和Rt△ODE中,由三角函数得出![]() ,由平行线得出△CAD∽△COE,得出
,由平行线得出△CAD∽△COE,得出![]() ,即可得出结果.
,即可得出结果.
(1)证明:连接![]()
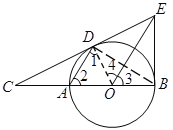
∵![]() ⊙
⊙![]() 的切线,
的切线,
∴![]()
∵![]() ∥
∥![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]() ≌
≌![]()
∴![]()
∵![]() 是⊙
是⊙![]() 的半径,
的半径,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(2)连接![]() ,设⊙
,设⊙![]() 的半径为
的半径为![]()
∵![]() ⊙
⊙![]() 的直径
的直径
∴![]()
在Rt![]() 中,
中, 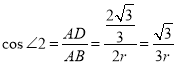
在Rt![]() 中,
中, ![]()
∵![]()
∴![]()
![]()
∴![]()
∵![]() ∥
∥![]()
∴![]() ∽
∽![]()
∴![]()
∴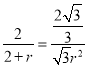
即![]()
解得![]() (不合题意,舍去)
(不合题意,舍去)
∴⊙![]() 的半径是
的半径是![]() .
.

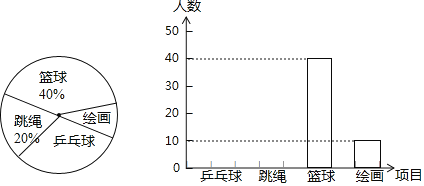
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)
频率分布表 | ||
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 10 | 0.20 |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | ||