题目内容
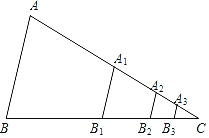
【题目】如图，△ABC的面积为4，分别取AC，BC两边的中点A1，B1，记△A1B1C的面积为S1；再分别取A1C，B1C的中点A2，B2，记△A2B2C的面积为S2，再分别取A2C，B2C的中点A3，B3，记△A3B3C的面积为S3；则S3的值等于_____．
【答案】
【解析】
根据三角形中位线定理得到A1B1＝
AB，A1B1∥AB，证明△CA1B1∽△CAB，根据相似三角形的性质计算，总结规律，根据规律解答即可．
解：∵点A1，B1是AC，BC两边的中点，
∴A1B1是△ABC的中位线，
∴A1B1＝AB，A1B1∥AB，
∴△CA1B1∽△CAB，
∴
＝（
）2＝
，
∵△ABC的面积为4，
∴S1＝1，
同理可得，S3＝，
故答案为：．
本题考查的是三角形中位线定理、相似三角形的判定和性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
练习册系列答案
相关题目
