题目内容
【题目】如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB折叠得到△ABD,交⊙O于点D.连接CD交AB于点E,延长BD和CA相交于点P,过点A作AG∥CD交BP于点G.
(1)求证:直线GA是⊙O的切线;
(2)求证:AC2=GDBD;
(3)若tan∠AGB=![]() ,PG=6,求cos∠P的值.
,PG=6,求cos∠P的值.
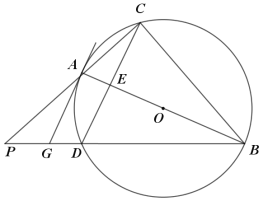
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)欲证明直线GA是⊙O的切线,只需推知OA⊥GA即可;
(2)根据折叠的性质得到:AC=AD.通过相似三角形△BAD∽△AGD的对应边成比例得到:![]() .所以AC2=AD2=GDBD.
.所以AC2=AD2=GDBD.
(3)cos∠P=![]() ,所以需要求得线段PD、PA的长度;利用(2)中的AD2=GDBD和锐角三角函数的定义求得BD=2GD;根据△PAG∽△PBA是对应边成比例得到:PA2=PGPB,即PA2=6(6+3GD);结合勾股定理知PA2=AD2+PD2.所以6(6+3GD)=(
,所以需要求得线段PD、PA的长度;利用(2)中的AD2=GDBD和锐角三角函数的定义求得BD=2GD;根据△PAG∽△PBA是对应边成比例得到:PA2=PGPB,即PA2=6(6+3GD);结合勾股定理知PA2=AD2+PD2.所以6(6+3GD)=(![]() )2+(6+GD)2.利用方程思想求得答案.
)2+(6+GD)2.利用方程思想求得答案.
(1)证明:∵将△ABC沿直线AB折叠得到△ABD,
∴BC=BD.
∴点B在CD的垂直平分线上.
同理得:点A在CD的垂直平分线上.
∴AB⊥CD即OA⊥CD,
∵AG∥CD.
∴OA⊥GA.
∵OA是⊙O的半径,
∴直线GA是⊙O的切线;
(2)证明:∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°.
∴∠ABD+∠BAD=90°.
∵∠GAB=90°,
∴∠GAD+∠BAD=90°.
∴∠ABD=∠GAD.
∵∠ADB=∠ADG=90°,
∴△BAD∽△AGD.
∴![]() .
.
∴AD2=GDBD.
∵AC=AD,
∴AC2=GDBD;
(3)解:∵tan∠AGB=![]() ,∠ADG=90°,
,∠ADG=90°,
∴![]() .
.
∴![]() .
.
∵AD2=GDBD,
∴BD=2GD.
∵![]() =
=![]() ,
,
∴∠GAD=∠GBA=∠PCD.
∵AG∥CD,
∴∠PAG=∠PCD.
∴∠PAG=∠PBA.
∵∠P=∠P,
∴△PAG∽△PBA.
∴PA2=PGPB
∵PG=6,BD=2GD,
∴PA2=6(6+3GD).
∴PA2=AD2+PD2.
∴6(6+3GD)=(![]() )2+(6+GD)2.
)2+(6+GD)2.
解得:GD=2或GD=0(舍去).
∴PD=8,AP=6![]() ,
,
∴cos∠P=![]() .
.