题目内容
【题目】如图1,在平面直角坐标系中,直线l1:y=2x+8与坐标轴分别交于A,B两点,点C在x正半轴上,且OA=OC.点P为线段AC(不含端点)上一动点,将线段OP绕点O逆时针旋转90°,得线段OQ(见图2)
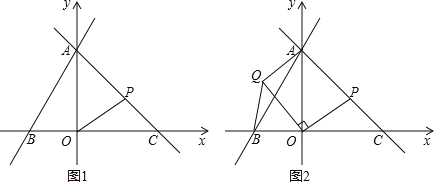
(1)分别求出点B、点C的坐标;
(2)如图2,连接AQ,求证:∠OAQ=45°;
(3)如图2,连接BQ,试求出当线段BQ取得最小值时点Q的坐标.
【答案】(1)B(-4,0),C(8,0);(2)详见解析;(3)点Q坐标为(-6,2).
【解析】
(1)利用待定系数法即可解决问题;
(2)只要证明△OAQ≌△OPC,可得∠OAQ=∠OCP=45°;
(3)因为∠OAQ=45°,设直线AQ交x轴与E,则点Q在直线AE上 运动,根据垂线段最短可知当BQ⊥AE时,BQ的长最短,求出直线AE、BQ的解析式,利用方程组确定交点Q的坐标即可;
解:(1)对于直线y=2x+8令x=0得到y=8,令y=0,得到x=-4,
∴A(0,8),B(-4,0),
∴OA=OC=8,
∴C(8,0).
(2)由旋转可知,OP=OQ,∠POQ=∠AOC=90°,
∴∠AOQ=∠COP,
在△AOQ和△COP中,
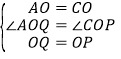 ,
,
∴△OAQ≌△OPC,
∴∠OAQ=∠OCP,
∵OA=OC,∠AOC=90°,
∴∠OCA=45°,
∴∠OAQ=45°.
(3)如图2中,
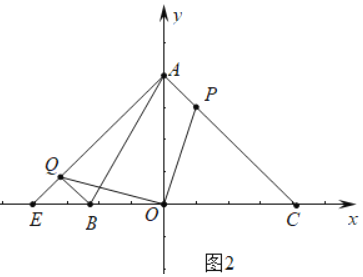
∵∠OAQ=45°,设直线AQ交x轴与E,则点Q在直线AE上运动,
∵A(0,8),E(-8,0),
∴直线AE的解析式为y=x+8,
根据垂线段最短可知当BQ⊥AE时,BQ的长最短,
∵BQ⊥AE,
∴直线BQ的解析式为y=-x-4,
由![]() ,解得
,解得![]() ,
,
∴当BQ最短时,点Q坐标为(-6,2).

练习册系列答案
相关题目