题目内容
【题目】一个不透明的口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)请用树状图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出球上的数字的积为奇数的概率.
【答案】(1)所有可能的结果共有9种,这些结果出现的可能性相等;(2)![]() .
.
【解析】
试题分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)可求得两次摸出的球上的数字积为奇数有4种情况,再利用概率公式即可求得答案
解:(1)根据题意,可以画如下的树状图:
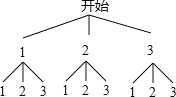
由树状图可以看出,所有可能的结果共有9种,这些结果出现的可能性相等;
(2)由(1)得:其中两次摸出的球上的数字积为奇数的有4种情况,
场P(两次摸出的球上的数字积为奇数)=![]() .
.

练习册系列答案
相关题目